
【题目】设函数f(x)=ax2+(b﹣1)x+3.
(1)若不等式f(x)>0的解为(﹣1, ![]() ),求不等式bx2﹣3x+a≤0的解集;
),求不等式bx2﹣3x+a≤0的解集;
(2)若f(1)=4,a>0,b>0,求ab的最大值.
【答案】
(1)解:若不等式f(x)>0的解为(﹣1, ![]() ),
),
可得﹣1, ![]() 是ax2+(b﹣1)x+3=0的两根,
是ax2+(b﹣1)x+3=0的两根,
即有﹣1+ ![]() =﹣
=﹣ ![]() ,﹣
,﹣ ![]() =
= ![]() ,
,
解得a=﹣2,b=2,
不等式bx2﹣3x+a≤0即为2x2﹣3x﹣2≤0,
解得﹣ ![]() ≤x≤2,
≤x≤2,
即解集为[﹣ ![]() ,2]
,2]
(2)解:f(1)=4,即为a+b=2,
由a>0,b>0,可得a+b≥2 ![]() ,
,
则ab≤1,当且仅当a=b=1取得最大值1.
即有ab的最大值为1.
【解析】1、由不等式的解集与一元二次方程根之间的关系,利用韦达定理可求出a=﹣2,b=2,得到新的不等式,解出即得结果。
2、由已知条件可得a+b=2,根据基本不等式求最值可得ab≤1,当且仅当a=b=1取得最大值1.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值).


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a≠0).
(a≠0).
(1)已知函数f(x)在点(0,1)处的斜率为1,求a的值;
(2)求函数f(x)的单调区间;
(3)若a>0,g(x)=x2emx , 且对任意的x1 , x2∈[0,2],f(x1)≥g(x2)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求函数y=f(x)的最小正周期;
(2)已知△ABC中,角A,B,C的对边分别是a,b,c,且a,b,c成等比数列,求f(B)的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,
,
(1)若a=﹣1,求f(x)的单调区间;
(2)若f(x)有最大值3,求a的值.
(3)若f(x)的值域是(0,+∞),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)满足 ![]() f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数: ①f(x)=sin
f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数: ①f(x)=sin ![]() x,g(x)=cos
x,g(x)=cos ![]() x;
x;
②f(x)=x+1,g(x)=x﹣1;
③f(x)=x,g(x)=x2 ,
其中为区间[﹣1,1]上的正交函数的组数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在D上的函数,若存在区间[m,n]D,使函数f(x)在[m,n]上的值域恰为[km,kn],则称函数f(x)是k型函数.给出下列说法:①f(x)=3﹣ ![]() 不可能是k型函数; ②若函数y=﹣
不可能是k型函数; ②若函数y=﹣ ![]() x2+x是3型函数,则m=﹣4,n=0;
x2+x是3型函数,则m=﹣4,n=0;
③设函数f(x)=x3+2x2+x(x≤0)是k型函数,则k的最小值为 ![]() ;
;
④若函数y= ![]() (a≠0)是1型函数,则n﹣m的最大值为
(a≠0)是1型函数,则n﹣m的最大值为 ![]() .
.
下列选项正确的是( )
A.①③
B.②③
C.②④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.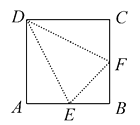
问:
(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com