
【题目】已知椭圆C:![]() 1(a>b>0)的右顶点为A(2,0),离心率为
1(a>b>0)的右顶点为A(2,0),离心率为![]() .
.
(1)求椭圆C的方程;
(2)设过点P(0,﹣2)的直线l与椭圆C相交于M,N两点,当△OMN的面积最大时(O为坐标原点),求直线l的方程.
【答案】(1)![]() 1(2)y
1(2)y![]() x﹣2.
x﹣2.
【解析】
(1)根据椭圆右顶点和离心率,结合![]() ,求得
,求得![]() 的值,由此求得椭圆方程.
的值,由此求得椭圆方程.
(2)设出直线![]() 的方程,联立直线方程和椭圆方程,写出韦达定理,利用弦长公式求得
的方程,联立直线方程和椭圆方程,写出韦达定理,利用弦长公式求得![]() ,利用点到直线的距离公式求得
,利用点到直线的距离公式求得![]() ,由此求得三角形
,由此求得三角形![]() 的面积的表达式,利用换元法,结合基本不等式,求得面积的最大值,以及此时直线
的面积的表达式,利用换元法,结合基本不等式,求得面积的最大值,以及此时直线![]() 的斜率,进而求得直线
的斜率,进而求得直线![]() 的方程.
的方程.
(1)由题意得:a=2,e![]() ,b2=a2﹣c2,解得:a2=2,b2=1,所以椭圆的方程为:
,b2=a2﹣c2,解得:a2=2,b2=1,所以椭圆的方程为:![]() 1;
1;
(2)由题意得直线l的斜率存在且不为零,设直线l的方程:y=kx﹣2,M(x,y),N(x',y'),联立与椭圆的方程整理得:(1+4k2)x2﹣16kx+12=0,△=(16k)2﹣4×12×(1+4k2)>0,得k2![]() ,x+x'
,x+x'![]() ,xx'
,xx'![]() ,所以弦长MN
,所以弦长MN![]() |x﹣x'|
|x﹣x'|![]() 4
4![]() ,原点到直线l的距离d
,原点到直线l的距离d![]() ,所以S△OMN
,所以S△OMN![]() MNd
MNd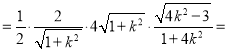
![]() ,令t
,令t![]() (t>0),所以4k2=t2+3, S
(t>0),所以4k2=t2+3, S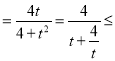 1,当且仅当t=2时等号成立,即k2
1,当且仅当t=2时等号成立,即k2![]() ,满足条件,解得k
,满足条件,解得k![]() ,所以直线l的方程为:y
,所以直线l的方程为:y![]() x﹣2.
x﹣2.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】设单调函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,如果单调函数
,如果单调函数![]() 使得函数
使得函数![]() 的值域也是
的值域也是![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的一个“保值域函数”.已知定义域为
的一个“保值域函数”.已知定义域为![]() 的函数
的函数![]() ,函数
,函数![]() 与
与![]() 互为反函数,且
互为反函数,且![]() 是
是![]() 的一个“保值域函数”,
的一个“保值域函数”,![]() 是
是![]() 的一个“保值域函数”,则
的一个“保值域函数”,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设min{m,n}表示m,n二者中较小的一个,已知函数f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
A.-4B.-3C.-2D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种零件的质量指标值以分数(满分100分)衡量,并根据分数的高低划分三个等级,如下表:

为了监控某种零件的一条生产线的生产过程,检验员随机抽取了100件零件,进行质量指标值检查,将检查结果进行整理得到如下的频率分布直方图:
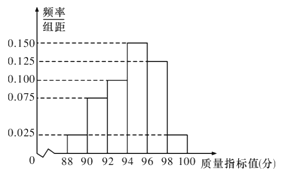
(1)若该生产线的质量指标值要求为:
第一条:生产线的质量指标值合格和优秀的零件至少要占全部零件的75%,
第二条:生产线的质量指标值平均分不低于95分;
如果同时满足以上两条就认定生产线的质量指标值合格,否则为不合格,请根据以上抽样调查数据,判断该生产线的质量指标值是否合格?
(2)在样本中,按质量指标值的等级用分层抽样的方法从质量指标值不合格和优秀的零件中抽取5件,再从这5件中随机抽取2件,求这两件的质量指标值恰好一个不合格一个优秀的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
A班 | 6 | 6.5 | 7 | |
B班 | 6 | 7 | 8 | |
C班 | 5 | 6 | 7 | 8 |
(1)试估计C班学生人数;
(2)从A班和B班抽出来的学生中各选一名,记A班选出的学生为甲,B班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二全体师生今秋开学前在新校区体验周活动中有优异的表现,学校拟对高二年级进行表彰;
(1)若要表彰3个优秀班级,规定从6个文科班中选一个,14个理科班中选两个班级,有多少种不同的选法?
(2)年级组拟在选出的三个班级中再选5名学生,每班至少1名,最多2名,则不同的分配方案有多少种?
(3)选中的这5名学生和三位年级负责人徐主任,陈主任,付主任排成一排合影留念,规定这3位老师不排两端,且老师顺序固定不变,那么不同的站法有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com