
分析 由向量垂直的条件和向量数量积的坐标表示,解释即可得到所求值.
解答 解:$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(1,1),且($\overrightarrow{a}$+$λ\overrightarrow{b}$)$⊥\overrightarrow{a}$,
可得$\overrightarrow{a}$2=1,$\overrightarrow{a}$•$\overrightarrow{b}$=1+0=1,
($\overrightarrow{a}$+λ$\overrightarrow{b}$)•$\overrightarrow{a}$=0,即有得$\overrightarrow{a}$2+λ$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即为1+λ=0,解得λ=-1.
故答案为:-1.
点评 本题考查向量的数量积的坐标表示和性质,考查向量的平方即为模的平方,以及向量垂直的条件,属于基础题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{9}=1$ | C. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | D. | $\frac{x^2}{2}+\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab<b2 | B. | ($\frac{1}{2}$)a>($\frac{1}{2}$)b | ||
| C. | log${\;}_{\frac{1}{2}}$a>log${\;}_{\frac{1}{2}}$b | D. | a2>b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | arcsin(-$\frac{\sqrt{2}}{10}$) | B. | arccos$\frac{\sqrt{2}}{10}$ | C. | arccos($\frac{\sqrt{2}}{10}$) | D. | -arccos$\frac{\sqrt{2}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
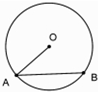
| A. | 18 | B. | -18 | C. | 36 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R,x2≥0”的否定为“?x0∈R,x2<0” | |
| B. | “a>b”是“ac2>bc2”的必要不充分条件 | |
| C. | “若x2-6x+5≠0,则x≠1”是真命题 | |
| D. | 命题p:A成立,命题q:B成立,则命题¬p∨¬q表示A,B至少有一个成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com