
【题目】有以下判断:①![]() 与
与![]() 表示同一函数;②函数
表示同一函数;②函数![]() 的图像与直线
的图像与直线![]() 最多有一个交点;③
最多有一个交点;③![]() 不是函数;④若点
不是函数;④若点![]() 在
在![]() 的图像上,则函数
的图像上,则函数![]() 的图像必过点
的图像必过点![]() .其中正确的判断有___________.
.其中正确的判断有___________.
【答案】②④
【解析】对于①,函数![]() 定义域为
定义域为![]() 且
且![]() ,而
,而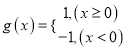 的定义域为
的定义域为![]() ,所以二者不是同一个函数,故①不正确;对于②,根据函数的定义,函数
,所以二者不是同一个函数,故①不正确;对于②,根据函数的定义,函数![]() 的图象与直线
的图象与直线![]() 的交点是
的交点是![]() 个或
个或![]() 个,即交点最多有一个,故②正确;对于③,
个,即交点最多有一个,故②正确;对于③, ![]() 是定义域为
是定义域为![]() 的函数,③错误;对于④,若点
的函数,③错误;对于④,若点![]() 在
在![]() 的图像上,必有
的图像上,必有![]() ,等价于
,等价于![]() ,即函数
,即函数![]() 的图像必过点
的图像必过点![]() ,④正确,综上,正确的判断是②④,,故答案为②④.
,④正确,综上,正确的判断是②④,,故答案为②④.
【 方法点睛】本题主要通过对多个命题真假的判断,综合考查函数的定义、函数的定义域、函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某厂每月生产一种投影仪的固定成本为![]() 万元,但每生产
万元,但每生产![]() 台,需要加可变成本(即另增加投入)
台,需要加可变成本(即另增加投入)![]() 万元,市场对此产品的月需求量为
万元,市场对此产品的月需求量为![]() 台,销售的收入函数为
台,销售的收入函数为![]() (万元)
(万元)![]() 且
且![]() ,其中
,其中![]() 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1)求月销售利润![]() (万元)关于月产量
(万元)关于月产量![]() (百台)的函数解析式;
(百台)的函数解析式;
(2)当月产量为多少时,销售利润可达到最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.
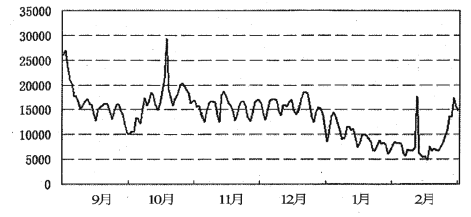
根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,四边形![]() 为正方形,AD∥B
为正方形,AD∥B![]() ,平面ABC⊥平面BC
,平面ABC⊥平面BC![]() ,AB=AC=
,AB=AC=![]() ,AD=1,∠ABC=45°。
,AD=1,∠ABC=45°。

(1)求证:AB⊥CD;
(2)求点C到平面D![]() 的距离。
的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 设直线l经过点
设直线l经过点![]() 且与椭圆C交于不同的两点M,N试问:在x轴上是否存在点Q,使得直线QM与直线QN的斜率的和为定值?若存在,求出点Q的坐标及定值,若不存在,请说明理由.
且与椭圆C交于不同的两点M,N试问:在x轴上是否存在点Q,使得直线QM与直线QN的斜率的和为定值?若存在,求出点Q的坐标及定值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c.满足2acosC+bcosC+ccosB=0.
(Ⅰ)求角C的大小;
(Ⅱ)若a=2,△ABC的面积为![]() ,求C的大小。
,求C的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭园C: ![]() +
+![]() =1(a>b>0)的左、右焦点分别为F1,F2.且椭圆C过点(
=1(a>b>0)的左、右焦点分别为F1,F2.且椭圆C过点(![]() ,-
,-![]() ),离心率e=
),离心率e=![]() ;点P在椭圆C 上,延长PF1与椭圆C交于点Q,点R是PF2中点.
;点P在椭圆C 上,延长PF1与椭圆C交于点Q,点R是PF2中点.
(I )求椭圆C的方程;
(II )若O是坐标原点,记△QF1O与△PF1R的面积之和为S,求S的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点A(-![]() ,0),B(
,0),B(![]() ,0),动点P在y轴上的投影是Q,且
,0),动点P在y轴上的投影是Q,且![]() .
.
(1)求动点P的轨迹C的方程;
(2)过F(1,0)作互相垂直的两条直线交轨迹C于点G,H,M,N,且E1,E2分别是GH,MN的中点.求证:直线E1E2恒过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com