【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，以坐标原点
为极点，以
轴正半轴为极轴，建立极坐标系，直线
的极坐标方程为
， 
的极坐标方程为
.
（1）求直线
与
的交点的轨迹
的方程；
（2）若曲线
上存在4个点到直线
的距离相等，求实数
的取值范围.
ABC考王全优卷系列答案科目：高中数学 来源： 题型：
【题目】2018年9月16日下午5时左右，今年第22号台风“山竹”在广东江门川岛镇附近正面登陆，给当地人民造成了巨大的财产损失，某记者调查了当地某小区的100户居民由于台风造成的经济损失，将收集的数据分成
，
，
，
，
五组，并作出如下频率分布直方图.
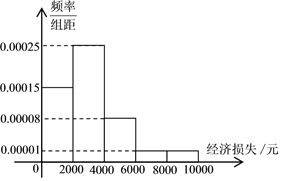
（Ⅰ）根据频率分布直方图估计该小区居民由于台风造成的经济损失的众数和平均值.
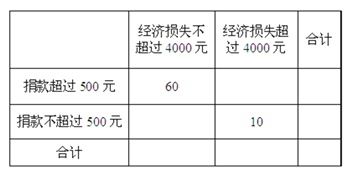
（Ⅱ）“一方有难，八方支援”，台风后居委会号召小区居民为台风重灾区捐款，
记者调查的100户居民捐款情况如下表格，在表格空白处填写正确数字，并说明是否有99%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
（Ⅲ）将上述调查所得到的频率视为概率，现在从该地区大量受灾居民中，采用随机抽样方法每次抽取1户居民，抽取3次，记被抽取的3户居民中自身经济损失超过
元的人数为
，若每次抽取的结果是相互独立的，求的分布列及期望
.
参考公式：
，其中
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的焦点为
，直线
与抛物线
交于
两点．
（Ⅰ）若直线
过焦点
，且与圆
交于
（其中
在
轴同侧），求证： 
是定值；
（Ⅱ）设抛物线
在
和
点的切线交于点
，试问： 
轴上是否存在点
，使得
为菱形？若存在，请说明理由并求此时直线
的斜率和点
的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高校数学与统计学院为了对2018年录取的大一新生有针对性地进行教学.从大一新生中随机抽取40名，对他们在2018年高考的数学成绩进行调查，统计发现40名新生的数学分数
分布在
内.当
时，其频率
.
（Ⅰ）求
的值；
（Ⅱ）请在答题卡中画出这40名新生高考数学分数的频率分布直方图，并估计这40名新生的高考数学分数的平均数；
（Ⅲ）从成绩在100～120分的学生中，用分层抽样的方法从中抽取5名学生，再从这5名学生中随机选两人甲、乙，记甲、乙的成绩分别为
，求概率
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝1－
(a>0，a≠1)且f(0)＝0.
(1)求a的值；
(2)若函数g(x)＝(2x＋1)·f(x)＋k有零点，求实数k的取值范围；
(3)当x∈(0，1)时，f(x)>m·2x－2恒成立，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】高三一班、二班各有6名学生去参加学校组织的高中数学竞赛选拔考试，成绩如茎叶图所示.
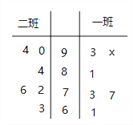
（1）若一班、二班6名学生的平均分相同，求
值；
（2）若将竞赛成绩在
、
、
内的学生在学校推优时，分别赋分、2分、3分，现在从一班的6名参赛学生中选两名，求推优时，这两名学生赋分的和为4分的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
、
的坐标分别是
，
，直线
，
相交于点
，且它们的斜率之积为
.
（1）求动点的轨迹方程；
（2）若过点
的直线
交动点的轨迹于
、
两点， 且
为线段，的中点，求直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
