
【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.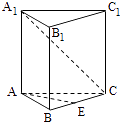
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.
【答案】
(1)解:过E作EN⊥AC于N,连接EF,NF,AC1,由直棱柱的性质可知,底面ABC⊥侧面A1C
∴EN⊥侧面A1C
NF为EF在侧面A1C内的射影
则由 ![]() ,得NF∥AC1,又AC1⊥A1C,故NF⊥A1C
,得NF∥AC1,又AC1⊥A1C,故NF⊥A1C
由三垂线定理可知EF⊥A1C
(2)解:连接AF,过N作NM⊥AF与M,连接ME
由(1)可知EN⊥侧面A1C,根据三垂线定理得EM⊥AF
∴∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=θ
设∠FAC=α则0°<α≤45°,
在直角三角形CNE中,NE= ![]() ,在直角三角形AMN中,MN=3sinα
,在直角三角形AMN中,MN=3sinα
故tanθ= ![]() ,又0°<α≤45°∴0<sinα≤
,又0°<α≤45°∴0<sinα≤ ![]()
故当α=45°时,tanθ达到最小值,
tanθ= ![]() ,此时F与C1重合.
,此时F与C1重合.
【解析】(1)过E作EN⊥AC于N,连接EF,NF,AC1 , 根据面面垂直的性质可知NF为EF在侧面A1C内的射影,根据 ![]() ,得NF∥AC1 , 又AC1⊥A1C,故NF⊥A1C,由三垂线定理可得结论;(2)连接AF,过N作NM⊥AF与M,连接ME根据三垂线定理得EM⊥AF,则∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=θ,在直角三角形CNE中,求出NE,在直角三角形AMN中,求出MN,故tanθ=
,得NF∥AC1 , 又AC1⊥A1C,故NF⊥A1C,由三垂线定理可得结论;(2)连接AF,过N作NM⊥AF与M,连接ME根据三垂线定理得EM⊥AF,则∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=θ,在直角三角形CNE中,求出NE,在直角三角形AMN中,求出MN,故tanθ= ![]() ,根据α的范围可求出最小值.
,根据α的范围可求出最小值.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() ,与
,与![]() ,
, ![]() 各有一个交点,当
各有一个交点,当![]() 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当![]() ,这两个交点重合.
,这两个交点重合.
(1)分别说明![]() ,
, ![]() 是什么曲线,并求出
是什么曲线,并求出![]() 与
与![]() 的值;
的值;
(2)设当![]() 时,
时, ![]() 与
与![]() ,
, ![]() 的交点分别为
的交点分别为![]() ,当
,当![]() ,
, ![]() 与
与![]() ,
, ![]() 的交点分别为
的交点分别为![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣1)ex﹣kx2(k∈R).
(1)当k=1时,求函数f(x)的单调区间;
(2)当 ![]() 时,求函数f(x)在[0,k]上的最大值M.
时,求函数f(x)在[0,k]上的最大值M.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C所对的边分别是a、b、c,且a+b+c=8.
(1)若a=2,b= ![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2 ![]() +sinBcos2
+sinBcos2 ![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S= ![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如图所示.食堂某天购进了 90个面包,以![]() (个)(其中
(个)(其中![]() )表示面包的需求量,
)表示面包的需求量, ![]() (元)表示利润.
(元)表示利润.
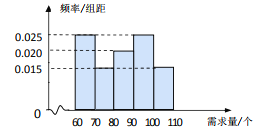
(1)根据直方图计算需求量的中位数;
(2)估计利润![]() 不少于100元的概率;
不少于100元的概率;
(3)在直方图的需求量分组中,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有1000个座位,票价不分等次,根据影院的经营经验,当每张票价不超过10元时,票可全售出;当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院定一个合适的票价,需符合的基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放一场电影的成本费用支出为5750元,票房的收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入) 问:
(1)把y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,票价定为多少时,放映一场的净收人最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an} 中,a1=1,a2= ![]() ,且
,且 ![]() (n=2,3,4,…)
(n=2,3,4,…)
(1)求a3、a4的值;
(2)设bn= ![]() (n∈N*),试用bn表示bn+1并求{bn} 的通项公式;
(n∈N*),试用bn表示bn+1并求{bn} 的通项公式;
(3)设cn= ![]() (n∈N*),求数列{cn}的前n项和Sn .
(n∈N*),求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高![]() 为
为![]() 米,它所占水平地面的长
米,它所占水平地面的长![]() 为
为![]() 米.该广告画最高点
米.该广告画最高点![]() 到地面的距离为
到地面的距离为![]() 米,最低点
米,最低点![]() 到地面距离
到地面距离![]() 米.假设某人眼睛到脚底的距离
米.假设某人眼睛到脚底的距离![]() 为
为![]() 米,他竖直站在此电梯上观看
米,他竖直站在此电梯上观看![]() 视角为
视角为![]() .
.
(Ⅰ)设此人到直线![]() 的距离为
的距离为![]() 米,试用含
米,试用含![]() 的表达式表示
的表达式表示![]() ;
;
(Ⅱ)此人到直线![]() 的距离为多少米时,视角
的距离为多少米时,视角![]() 最大?
最大?
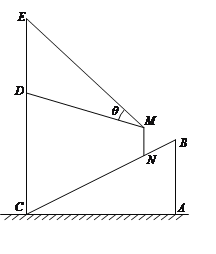
查看答案和解析>>
科目:高中数学 来源: 题型:
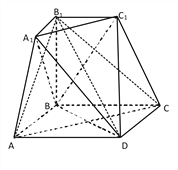
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com