
【题目】已知四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() 底面
底面![]() ,
,![]() 是
是![]() 上的任意一点
上的任意一点

![]() 求证:平面
求证:平面![]() 平面
平面![]()
![]() 设
设![]() ,求点
,求点![]() 到平面
到平面![]() 的距离
的距离
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,求
,求![]() 与平面
与平面![]() 所成角的正切值
所成角的正切值
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:

(1)求回归直线方程![]() ,其中
,其中![]() ,
,![]() .
.
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=asinθ,直线l的参数方程是 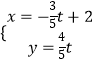 (t为参数)
(t为参数)
(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;
(2)直线l被圆C截得的弦长等于圆C的半径的 ![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,
,![]() 是函数
是函数![]() 图象上任意不同的两点,线段
图象上任意不同的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .证明:
.证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生暑假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
|
|
|
|
| |
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
(![]() )从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为
)从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为![]() 的概率?
的概率?
(![]() )若从阅读名著不少于
)若从阅读名著不少于![]() 本的学生中任选
本的学生中任选![]() 人,设选到的男学生人数为
人,设选到的男学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
(![]() )试判断男学生阅读名著本数的方差
)试判断男学生阅读名著本数的方差![]() 与女学生阅读名著本数的方程
与女学生阅读名著本数的方程![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() (
(![]() 为参数)与曲线
为参数)与曲线![]() 相交于
相交于![]() 两点.
两点.
(I)试写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查![]() 结果只有“满意”和“不满意”两种
结果只有“满意”和“不满意”两种![]() ,从被调查的学生中随机抽取了50人,具体的调查结果如表:
,从被调查的学生中随机抽取了50人,具体的调查结果如表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 5 | 9 | 11 | 9 | 7 | 9 |
满意人数 | 4 | 7 | 8 | 5 | 6 | 6 |
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com