
| A. | $f(x)={log_2}(\sqrt{{x^2}+1}-x)$ | B. | $f(x)=\frac{1}{x}$ | C. | f(x)=x2-x3 | D. | f(x)=sinx |
分析 根据函数的奇偶性定义、对数函数的单调性、复合函数的单调性判断A;根据基本初等函数奇偶性和单调性的性质分别判断B、C、D即可.
解答 解:A.$f(x)=lo{g}_{2}(\sqrt{{x}^{2}+1}-x)$的定义域是R,
且$f(-x)=lo{g}_{2}(\sqrt{{x}^{2}+1}+x)$=$lo{g}_{2}(\sqrt{{x}^{2}+1}-x)^{-1}$=-f(x),
所以f(x)是奇函数,
因为y=$\sqrt{{x}^{2}+1}-x$=$\frac{1}{\sqrt{{x}^{2}+1}+x}$在定义域上是减函数,
所以函数$f(x)=lo{g}_{2}(\sqrt{{x}^{2}+1}-x)$在定义域上是减函数,满足条件;
B.$f(x)=\frac{1}{x}$是定义域{x|x≠0}上的奇函数,在(-∞,0),(0,+∞)上是减函数,
但是在定义域上不是减函数,不满足条件;
C.因为f(-x)=(-x)2-(-x)3=x2+x3,所以f(x)是非奇非偶函数,不满足条件;
D.f(x)=sinx是奇函数,在定义域上不是单调函数,不满足条件.
故选:A.
点评 本题考查函数奇偶性和单调性的判断,以及对数函数的单调性、复合函数的单调性,熟练掌握常见函数的奇偶性和单调性是解题的关键.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
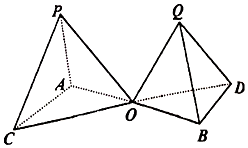 如图所示的“相邻塔”形立体建筑,已知P-OAC和Q-OBD是边长分别为a和$\frac{m}{a}({m是常数})$的两个正四面体,底面中AB与CD交于点O,试求出塔尖P,Q之间的距离关于边长a的函数,并求出a为多少时,塔尖P,Q之间的距离最短.
如图所示的“相邻塔”形立体建筑,已知P-OAC和Q-OBD是边长分别为a和$\frac{m}{a}({m是常数})$的两个正四面体,底面中AB与CD交于点O,试求出塔尖P,Q之间的距离关于边长a的函数,并求出a为多少时,塔尖P,Q之间的距离最短.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | $\frac{28}{3}$ | C. | $\frac{32}{3}$ | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com