
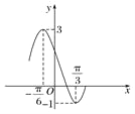
【题目】已知函数g(x)=Acos(ωx+φ)+B的部分图象如图所示,将函数g(x)的图象保持纵坐标不变,横坐标向右平移![]() 个单位长度后得到函数f(x)的图象.求:
个单位长度后得到函数f(x)的图象.求:
(1)函数f(x)在![]() 上的值域;
上的值域;
(2)使f(x)≥2成立的x的取值范围.
【答案】(1) [0,3] (2)![]()
【解析】
(1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数g(x)的解析式.再根据函数y=Acos(ωx+φ)+B的图象的平移变换规律,可得f(x)的解析式,再根据x∈[![]() ,
,![]() ],利用余弦函数的定义域和值域求得可得f(x)的值域;
],利用余弦函数的定义域和值域求得可得f(x)的值域;
(2)由f(x)≥2可得 cos(2x![]() )
)![]() ,故有2kπ
,故有2kπ![]() 2x
2x![]() 2kπ
2kπ![]() ,k∈z,由此求得不等式的解集.
,k∈z,由此求得不等式的解集.
(1)由图知B=![]() =1,A=
=1,A=![]() =2,T=2(
=2,T=2(![]() )=π,
)=π,
所以ω=2,所以g(x)=2cos(2x+φ)+1.
把(![]() )代入,得2cos(
)代入,得2cos(![]() )+1=-1,
)+1=-1,
即![]() +φ=π+2kπ(k∈Z),
+φ=π+2kπ(k∈Z),
所以φ=2kπ+![]() (k∈Z).
(k∈Z).
因为|φ|<![]() ,所以φ=
,所以φ=![]() ,
,
所以g(x)=2cos(2x+![]() )+1,
)+1,
所以f(x)=2cos(2x-![]() )+1.
)+1.
因为x∈![]() ,所以2x-
,所以2x-![]() ∈
∈![]() ,
,
所以f(x)∈[0,3],即函数f(x)在![]() 上的值域为[0,3].
上的值域为[0,3].
(2)因为f(x)=2cos(2x-![]() )+1,
)+1,
所以2cos(2x-![]() )+1≥2,
)+1≥2,
所以cos(2x-![]() )≥
)≥![]() ,
,
所以-![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2kπ(k∈Z),
+2kπ(k∈Z),
所以kπ≤x≤kπ+![]() (k∈Z),
(k∈Z),
所以使f(x)≥2成立的x的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】轮船在海上航行时,需要借助无线电导航确认自己所在的位置,以把握航向.现有![]() 、
、![]() 、
、![]() 三个无线电发射台,其中
三个无线电发射台,其中![]() 在陆地上,
在陆地上,![]() 在海上,
在海上,![]() 在某国海岸线上,(该国这段海岸线可以近似地看作直线的一部分),如下图.已知
在某国海岸线上,(该国这段海岸线可以近似地看作直线的一部分),如下图.已知![]() 、
、![]() 两点距离10千米,
两点距离10千米,![]() 是
是![]() 的中点,海岸线与直线
的中点,海岸线与直线![]() 的夹角为
的夹角为![]() .为保证安全,轮船的航路始终要满足:接收到
.为保证安全,轮船的航路始终要满足:接收到![]() 点的信号比接收到
点的信号比接收到![]() 点的信号晚
点的信号晚![]() 秒.(注:无线电信号每秒传播
秒.(注:无线电信号每秒传播![]() 千米).在某时刻,测得轮船距离
千米).在某时刻,测得轮船距离![]() 点距离为4千米.
点距离为4千米.

(1)以点![]() 为原点,直线
为原点,直线![]() 为
为![]() 轴建立平面直角坐标系(如图),求出该时刻轮船的位置;
轴建立平面直角坐标系(如图),求出该时刻轮船的位置;
(2)根据经验,船只在距离海岸线1.5千米以内的海域航行时,有搁浅的风险.如果轮船保持目前的航路不变,那么是否有搁浅风险?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一个正方体![]() 与一个半球
与一个半球![]() 构成的组合体,半球
构成的组合体,半球![]() 的底面圆与该正方体的上底面
的底面圆与该正方体的上底面![]() 的四边相切,
的四边相切, ![]() 与正方形
与正方形![]() 的中心重合.将此组合体重新置于一个球
的中心重合.将此组合体重新置于一个球![]() 中(球
中(球![]() 未画出),使该正方体的下底面
未画出),使该正方体的下底面![]() 的顶点均落在球
的顶点均落在球![]() 的表面上,半球
的表面上,半球![]() 与球
与球![]() 内切,设切点为
内切,设切点为![]() ,若正四棱锥
,若正四棱锥![]() 的表面积为
的表面积为![]() ,则球
,则球![]() 的表面积为( )
的表面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com