
【题目】已知定义在R上的连续函数g(x)满足:①当x>0时,g′(x)>0恒成立(g′(x)为函数g(x)的导函数);②对任意的x∈R都有g(x)=g(﹣x),又函数f(x)满足:对任意的x∈R,都有 ![]() 成立.当
成立.当 ![]() 时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤g(a2﹣a+2)对x∈[﹣
时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤g(a2﹣a+2)对x∈[﹣ ![]() ,
, ![]() ]恒成立,则a的取值范围是( )
]恒成立,则a的取值范围是( )
A.a∈R
B.0≤a≤1
C.![]()
D.a≤0或a≥1
【答案】D
【解析】解:因为函数g(x)满足:当x>0时,g′(x)>0恒成立且对任意x∈R都有g(x)=g(﹣x),
则函数g(x)为R上的偶函数且在[0,+∞)上为单调递增函数,且有g(|x|)=g(x),
所以g[f(x)]≤g(a2﹣a+2)在R上恒成立|f(x)|≤|a2﹣a+2|对x∈[﹣ ![]() ﹣2
﹣2 ![]() ,
, ![]() +2
+2 ![]() ]恒成立,
]恒成立,
只要使得定义域内|f(x)|max≤|a2﹣a+2|min , 由于当x∈[﹣ ![]() ,
, ![]() ]时,f(x)=x3﹣3x,
]时,f(x)=x3﹣3x,
求导得:f′(x)=3x2﹣3=3(x+1)(x﹣1),该函数过点(﹣ ![]() ,0),(0,0),(
,0),(0,0),( ![]() ,0),
,0),
且函数在x=﹣1处取得极大值f(﹣1)=2,在x=1处取得极小值f(1)=﹣2,
又由于对任意的x∈R都有f( ![]() +x)=﹣f(x)f(2
+x)=﹣f(x)f(2 ![]() +x)=﹣f(
+x)=﹣f( ![]() +x)=f(x)成立,
+x)=f(x)成立,
则函数f(x)为周期函数且周期为T=2 ![]() ,
,
所以函数f(x)在x∈[﹣ ![]() ,
, ![]() ]的最大值为2,
]的最大值为2,
所以令2≤|a2﹣a+2|解得:a≥1或a≤0.
故选:D.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,根据市场调查与市场预测,A产品的利润与投资成正比,其关系如图(1);B产品的利润与投资的算术平方根成正比,其关系如图(2)(注:所示图中的横坐标表示投资金额,单位为万元) 
(1)分别求出A,B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届湖北省黄冈市高三上学期期末考试第16题) “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”. “中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2017这2016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列![]() ,则此数列的项数为__________.
,则此数列的项数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校的平面示意图为如下图五边形区域![]() ,其中三角形区域
,其中三角形区域![]() 为生活区,四边形区域
为生活区,四边形区域![]() 为教学区,
为教学区, ![]() 为学校的主要道路(不考虑宽度).
为学校的主要道路(不考虑宽度). ![]() .
.
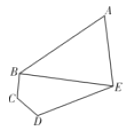
(1)求道路![]() 的长度;(2)求生活区
的长度;(2)求生活区![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了了解树苗生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米).把这些高度列成了如下的频率分布表:

(1)在这批树苗中任取一棵,其高度不低于80厘米的概率大约是多少?
(2)这批树苗的平均高度大约是多少?(用各组的中间值代替各组数据的平均值)
(3)为了进一步获得研究资料,若从![]() 组中移出一棵树苗,从
组中移出一棵树苗,从![]() 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则![]() 组中的树苗
组中的树苗![]() 和
和![]() 组中的树苗
组中的树苗![]() 同时被移出的概率是多少?
同时被移出的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,小华和小明两个小伙伴在一起做游戏,他们通过划拳(剪刀、石头、布)比赛决胜谁首先登上第3个台阶,他们规定从平地开始,每次划拳赢的一方登上一级台阶,输的一方原地不动,平局时两个人都上一级台阶,如果一方连续两次赢,那么他将额外获得一次上一级台阶的奖励,除非已经登上第3个台阶,当有任何一方登上第3个台阶时,游戏结束,记此时两个小伙伴划拳的次数为![]() .
.

(1)求游戏结束时小华在第2个台阶的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com