
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
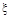 ,那么
,那么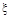 =4表示的随机试验结果是( )
=4表示的随机试验结果是( )| A.一颗是3点,一颗是1点 | B.两颗都是2点 |
| C.两颗都是4点 | D.一颗是3点,一颗是1点或两颗都是2点 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
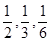 ,在一段时间内该电话机共打进三个电话,且各个电话之间相互独立,则这三个电话中恰有两个是打给乙的概率是 (用分数作答)
,在一段时间内该电话机共打进三个电话,且各个电话之间相互独立,则这三个电话中恰有两个是打给乙的概率是 (用分数作答)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
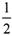 ,丙、丁两人各自闯关成功的概率均为
,丙、丁两人各自闯关成功的概率均为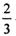 .
.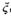 ,求
,求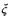 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
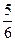 和
和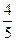 ,且各株大树是否成活互不影响。求移栽的4株大树中:
,且各株大树是否成活互不影响。求移栽的4株大树中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com