
| A�� | ����ٺ�����ڶ����� | B�� | ����ٺ�����ڶ������� | ||
| C�� | ����ٳ���������ڲ����� | D�� | ����ٲ�����������ڳ��� |
���� ����SΪSn�����Ӽ����������Ӽ���ż�Ӽ��Ķ��壬�õ����Ӽ���ż�Ӽ�֮��Ĺ�ϵ����������֤�ý��ۣ�
��������Ӽ�������֮�ͣ��Ӷ��õ�ż�Ӽ�������֮�ͣ����ɵõ����ۣ�
��� �⣺����SΪSn�����Ӽ�����T��ż�Ӽ���A��T�����Ӽ��ļ���ż�Ӽ���һһ��Ӧ������ÿ��ż�Ӽ�T����ǡ��һ�����Ӽ���֮��Ӧ����Sn�����Ӽ���ż�Ӽ�������ȣ���ȷ��
�ڶ���һi��1��i��n������i���Ӽ�����2n-1����Sn�����Ӽ���ż�Ӽ�������ȿ�֪��
��i��1ʱ����2n-1���Ӽ�����һ��ʱ���Ӽ���
��i=1ʱ������n��3�����ϱߵ�1����3��ͬ���ɵ�������һ��ʱ���Ӽ���
�����ڼ������Ӽ�����֮��ʱ�����Ӽ�����֮����$\sum_{i=1}^{n}$2n-2i=n��n+1��•2n-3��
����������˵����Ҳ��ż�Ӽ�������֮�ͣ�������ȣ�
�ʵ�n��3ʱ��Sn���������Ӽ�������֮�͵�������ż�Ӽ�������֮�ͣ���ȷ��
��ѡ��A��
���� ���⿼�鼯�ϵ��Ӽ������¶�������ͣ��ؼ�����ȷ�����桢ż�Ӽ��������ĸ���ڽ����̵��г���������¶�������Ĺ��ɡ��оٵķ�����������ת����˼�룮ֵ��ͬѧ����ᷴ˼���������⣮


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2ֻȫ�ǻ��ĸ��� | B�� | 2��ȫ�Ǻõĸ��� | ||
| C�� | ǡ��1ֻ�ǻ��ĸ��� | D�� | ����1ֻ�ǻ��ĸ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{16}$ | B�� | $\frac{3}{8}$ | C�� | $\frac{5}{8}$ | D�� | ��ͬ�����ϴ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18�� | B�� | 24�� | C�� | 30�� | D�� | 48�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
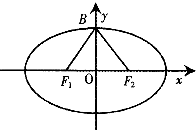 ��F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬BΪ�����һ���˵㣬�ҡ�F1BF2�DZ߳�Ϊ2�ĵȱ������Σ�
��F1��F2�ֱ�����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬BΪ�����һ���˵㣬�ҡ�F1BF2�DZ߳�Ϊ2�ĵȱ������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��n-1��2n+1-2 | B�� | ��n-1��2n+1+2 | C�� | ��n+1��2n+1-2 | D�� | ��n+1��2n+1+2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com