
【题目】已知数列{an}的前n项和Sn= ![]() n,
n,
(1)求通项公式an的表达式;
(2)令bn=an2n﹣1 , 求数列{bn}的前n项的和Tn .
【答案】
(1)解:当n≥2时,an=Sn﹣Sn﹣1= ![]() n﹣
n﹣ ![]() (n﹣1)2﹣
(n﹣1)2﹣ ![]() (n﹣1)=n,
(n﹣1)=n,
当n=1时,a1=S1=1也适合上式,
∴通项公式an的表达式为an=n
(2)解:bn=an2n﹣1=n2n﹣1,
∴Tn=120+2×21+…+(n﹣1)2n﹣2+n2n﹣1①
2Tn=121+222+…+(n﹣1)2n﹣1+n2n②
②﹣①得到,Tn=﹣(120+121+…+12n﹣1)+n2n=(n﹣1)2n+1
所以Tn=(n﹣1)2n+1
【解析】(1)因为给出了数列{an}的前n项和Sn= ![]() n,所以可用n≥2时,an=Sn﹣Sn﹣1来求数列{an}的通项公式,再判断n=1是否符合通项公式即可.(2)把(1)中求出的数列{an}的通项公式代入bn=an2n﹣1 , 求出数列{bn}的通项公式,再利用错位相减法求数列{bn}的前n项和Tn .
n,所以可用n≥2时,an=Sn﹣Sn﹣1来求数列{an}的通项公式,再判断n=1是否符合通项公式即可.(2)把(1)中求出的数列{an}的通项公式代入bn=an2n﹣1 , 求出数列{bn}的通项公式,再利用错位相减法求数列{bn}的前n项和Tn .
【考点精析】解答此题的关键在于理解等差数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() 或
或![]() ,以及对等差数列的前n项和公式的理解,了解前n项和公式:
,以及对等差数列的前n项和公式的理解,了解前n项和公式:![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】一支车队有![]() 辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午![]() 时出发,第二辆车于下午
时出发,第二辆车于下午![]() 时
时![]() 分出发,第三辆车于下午
分出发,第三辆车于下午![]() 时
时![]() 分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午![]() 时停下来休息.
时停下来休息.
到下午![]() 时,最后一辆车行驶了多长时间?
时,最后一辆车行驶了多长时间?
如果每辆车的行驶速度都是![]() ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,周长为7.5cm,且sinA:sinB:sinC=4:5:6,下列结论:
①a:b:c=4:5:6 ②a:b:c=2: ![]() ③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
其中成立的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 与定点
与定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() ,
,
(1)求点![]() 的轨迹曲线
的轨迹曲线![]() 的方程:
的方程:
(2)过定点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,以
两点,以![]() 三点(
三点(![]() 为坐标原点)为顶点作平行四边形
为坐标原点)为顶点作平行四边形![]() ,若点
,若点![]() 刚好在曲线
刚好在曲线![]() 上,求直线
上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S﹣ABCD的底面边长为2,高为2,E为边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为( )
A.![]()
B.![]()
C.3 ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过35微克/立方米,
的年平均浓度不得超过35微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天
的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.

(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)由频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教育机构随机某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是( ) 
A.
B.
C.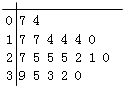
D.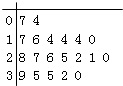
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【山东省实验中学2017届高三第一次诊断】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com