
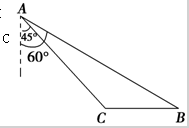
 如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?( | 2 |
| 3 |
| 6 |
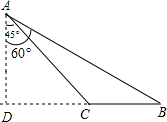 解:过点A作AD⊥BC的延长线于点D,
解:过点A作AD⊥BC的延长线于点D,
|
| 2 |
| 2 |
| 3 |
| 6 |
| 6 |
| 2 |
| AC |
| 30 |
| 1 |
| 3 |
| BC |
| 13 |
| 1 |
| 3 |


科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、2[x+1] |
| B、2([x]+1) |
| C、2{x} |
| D、{2x} |
查看答案和解析>>
科目:高中数学 来源: 题型:
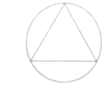 某人随机地向如图所示的正三角形及其外接圆区域内部设计(不包括三角形及其外接圆的边界),则针孔到正三角形内部(不包括边界)的概率为( )
某人随机地向如图所示的正三角形及其外接圆区域内部设计(不包括三角形及其外接圆的边界),则针孔到正三角形内部(不包括边界)的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
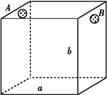 为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,当a、b各为( )米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?
为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,当a、b各为( )米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?| A、a=2,b=9 |
| B、a=9,b=2 |
| C、a=3,b=6 |
| D、a=6,b=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com