
【题目】梯形BDEF所在平面垂直于平面ABCD于BD,EF∥BD,EF=DE= ![]() BD,BD=BC=CD=
BD,BD=BC=CD= ![]() AB=
AB= ![]() AD=2,DE⊥BC.
AD=2,DE⊥BC.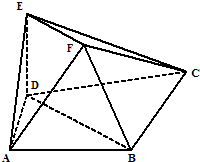
(1)求证:DE⊥平面ABCD;
(2)求平面AEF与平面CEF所成的锐二面角的余弦值.
【答案】
(1)
证明:连接AC,交BD于O,
∵BD=BC=CD,且AB=AD,∴AC⊥BD,
∵平面BDEF⊥平面ABCD,交线为BD,且AC平面ABCD,
∴AC⊥平面BDEF,
∵DE平面BDEF,∴DE⊥AC,
又DE⊥BC,且AC∩BC=C,∴DE⊥平面ABCD.
(2)
解:∵EF∥BD,EF= ![]() BD,且O是BD中点,∴ODEF是平行四边形,
BD,且O是BD中点,∴ODEF是平行四边形,
∴OF∥DE,∴OF⊥平面ABCD,
分别以OA,OB,OC为x轴,y轴,z轴建立空间直角坐标系,
A(1,0,0),C(﹣ ![]() ,0,0),E(0,﹣1,1),F(0,0,1),
,0,0),E(0,﹣1,1),F(0,0,1),
![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(0,1,0),
=(0,1,0), ![]() =(
=( ![]() ),
),
设平面AEF的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取x=1,得
,取x=1,得 ![]() =(1,0,1),
=(1,0,1),
设平面CEF的法向量 ![]() ,
,
则 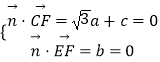 ,取a=1,得
,取a=1,得 ![]() =(1,0,﹣
=(1,0,﹣ ![]() ),
),
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() .
.
即平面AEF与平面CEF所成的锐二面角的余弦值为 ![]() .
.

【解析】(1)连接AC,交BD于O,推导出AC⊥BD,从而AC⊥平面BDEF,进而DE⊥AC,再由DE⊥BC,能证明DE⊥平面ABCD.(2)分别以OA,OB,OC为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出平面AEF与平面CEF所成的锐二面角的余弦值.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】【2017湖南长沙二模】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,
,![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() (
(![]() )的一条直线的两个端点.
)的一条直线的两个端点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() (
(![]() )相交于
)相交于![]() 两点,射线
两点,射线![]() ,
,![]() 与椭圆
与椭圆![]() 分别相交于点
分别相交于点![]() ,试探究:是否存在数集
,试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】荆州市某重点学校为了了解高一年级学生周末双休日在家活动情况,打算从高一年级1256名学生中抽取50名进行抽查,若采用下面的方法选取:先用简单随机抽样从1256人中剔除6人,剩下1250人再按系统抽样的方法进行,则每人入选的机会( )
A.不全相等
B.均不相等
C.都相等
D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1=﹣an2+2an , n∈N* , 且a1=0.9,令bn=lg(1﹣an);
(1)求证:数列{bn}是等比数列;
(2)求数列{ ![]() }各项和.
}各项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,离心率 ![]() ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线 ![]() 的焦点重合.
的焦点重合.
(1)求椭圆C的方程;
(2)过点S( ![]() ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017苏北四市一模19】已知函数![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)证明:![]() ;
;
(3)是否存在常数![]() ,使得
,使得![]() 对任意的
对任意的![]() 恒成立?若存在,求
恒成立?若存在,求
出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°.
(Ⅰ)证明AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人从一鱼池中捕得120条鱼,做了记号之后,再放回池中,经过适当的时间后,再从池中捕得100条鱼,结果发现有记号的鱼为10条(假定鱼池中不死鱼,也不增加),则鱼池中大约有鱼( )
A.120条
B.1200条
C.130条
D.1000条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com