
【题目】如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点.

求证:(1)E、C、D1、F四点共面;
(2)CE、D1F、DA三线共点.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)要证四点共线,可证明EF//CD1,根据推论三可得四点共面;(2)从图中可以看出AD是平面ABCD与平面ADD1A1的交线,说明D1F与CE相交,则交点在两平面的交线上,从而得三线共点
试题解析:
证明:(1)如图所示,连接CD1、EF、A1B,
∵E、F分别是AB和AA1的中点,
∴FE∥A1B且EF=![]() A1B.
A1B.
∵A1D1∥BC,A1D1=BC
∴四边形A1BCD1是平行四边形,
∴A1B∥D1C,∴FE∥D1C,
∴EF与CD1可确定一个平面,即E、C、D1、F四点共面.

(2)由(1)知EF∥CD1,且EF=![]() CD1,
CD1,
∴四边形CD1FE是梯形,
∴直线CE与D1F必相交,设交点为P,
则P∈CE平面ABCD,
且P∈D1F平面A1ADD1,
∴P∈平面ABCD且P∈平面A1ADD1.
又平面ABCD∩平面A1ADD1=AD,
∴P∈AD,∴CE、D1F、DA三线共点.


科目:高中数学 来源: 题型:
【题目】如图,点![]() 是圆
是圆![]() 内的一个定点,点
内的一个定点,点![]() 是圆
是圆![]() 上的任意一点,线段
上的任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() ,当点
,当点![]() 在圆
在圆![]() 上运动时,点
上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
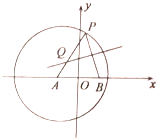
(1)求曲线![]() 的方程;
的方程;
(2)点![]() ,
, ![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输公司接受了向一地区每天至少运送180 t物资的任务,该公司有8辆载重为6 t的A型卡车和4辆载重为10 t的B型卡车,有10名驾驶员,每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的费用为A型卡车320元,B型卡车504元,则公司如何调配车辆,才能使公司所花的费用最低,最低费用为________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·山东)设f(x)=xlnx-ax2+(2a-1)x,a∈R.
(1)令g(x)=f′(x),求g(x)的单调区间;
(2)已知f(x)在x=1处取得极大值,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张纸的长、宽分别为2![]() a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是________(写出所有正确命题的序号).
a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是________(写出所有正确命题的序号).

①该多面体是三棱锥;②平面BAD⊥平面BCD;
③平面BAC⊥平面ACD;④该多面体外接球的表面积为5πa2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·洛阳市统考)已知数列{an}的前n项和为Sn,an≠0,a1=1,且2anan+1=4Sn-3(n∈N*).
(1)求a2的值并证明:an+2-an=2;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ex(ln x-a)(e是自然对数的底数,
e=2.71 828…).
(1)若y=f(x)在x=1处的切线方程为y=2ex+b,求a,b的值.
(2)若函数f(x)在区间![]() 上单调递减,求实数a的取值范围.
上单调递减,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,焦距为2c,且c,
,焦距为2c,且c, ![]() ,2成等比数列.
,2成等比数列.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)点B坐标为(0, ![]() ),问是否存在过点B的直线l交椭圆C于M,N两点,且满足
),问是否存在过点B的直线l交椭圆C于M,N两点,且满足![]() (O为坐标原点)?若存在,求出此时直线l的方程;若不存在,请说明理由.
(O为坐标原点)?若存在,求出此时直线l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com