
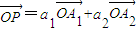 £¨«Ûa1+a2µƒ÷µ£ª
£¨«Ûa1+a2µƒ÷µ£ª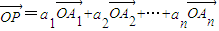 £¨Œ“√«≥∆
£¨Œ“√«≥∆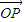 «œÚ¡ø
«œÚ¡ø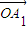 £¨
£¨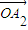 £¨°≠£¨
£¨°≠£¨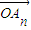 µƒœþ–‘◊È∫œ£¨{an} «∏√œþ–‘◊È∫œµƒœµ ˝ ˝¡–£Æµ±
µƒœþ–‘◊È∫œ£¨{an} «∏√œþ–‘◊È∫œµƒœµ ˝ ˝¡–£Æµ±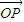 «œÚ¡ø
«œÚ¡ø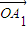 £¨
£¨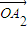 £¨°≠£¨
£¨°≠£¨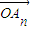 µƒœþ–‘◊È∫œ ±£¨«Î≤Œøº“‘œ¬œþÀ˜£∫
µƒœþ–‘◊È∫œ ±£¨«Î≤Œøº“‘œ¬œþÀ˜£∫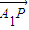 =¶À
=¶À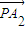 £®∆‰÷–¶À°Ÿ-1£©£ª”…œÚ¡øµƒœþ–‘‘ÀÀ„£¨µ√
£®∆‰÷–¶À°Ÿ-1£©£ª”…œÚ¡øµƒœþ–‘‘ÀÀ„£¨µ√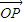 =
=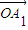 +
+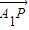 =
=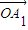 +
+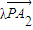 =
=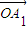 +¶À
+¶À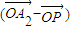 £ª’˚¿Ìø…µ√
£ª’˚¿Ìø…µ√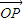 =
=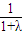
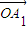 +
+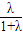
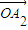 £ªº¥µ√a1+a2µƒ÷µ£ª
£ªº¥µ√a1+a2µƒ÷µ£ª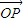 =a1
=a1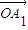 +a2
+a2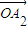 +°≠+an
+°≠+an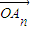 £¨‘Úx=a1x1+a2x2+°≠+anxn£¨µ±i+j=n+1 ±£¨”–ai=aj£¨À˘“‘x=anx1+an-1x2+°≠+a2xn-1+a1xn£¨‘Ú2x=a1£®x1+xn£©+a2£®x2+xn-1£©+°≠+an£®xn+x1£©£¨”… ˝¡–{xn} «µ»≤Ó ˝¡–£¨‘Úx1+xn=x2+xn-1=°≠=xn+x1£¨ø…µ√2x£¨¥”∂¯µ√x£¨Õ¨¿Ìµ√y£ªº¥µ√µ„P‘⁄÷±œþl…œ£Æ
£¨‘Úx=a1x1+a2x2+°≠+anxn£¨µ±i+j=n+1 ±£¨”–ai=aj£¨À˘“‘x=anx1+an-1x2+°≠+a2xn-1+a1xn£¨‘Ú2x=a1£®x1+xn£©+a2£®x2+xn-1£©+°≠+an£®xn+x1£©£¨”… ˝¡–{xn} «µ»≤Ó ˝¡–£¨‘Úx1+xn=x2+xn-1=°≠=xn+x1£¨ø…µ√2x£¨¥”∂¯µ√x£¨Õ¨¿Ìµ√y£ªº¥µ√µ„P‘⁄÷±œþl…œ£Æ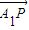 =¶À
=¶À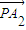 £®∆‰÷–¶À°Ÿ-1£©£ª
£®∆‰÷–¶À°Ÿ-1£©£ª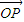 =
=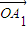 +
+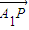 =
=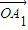 +
+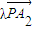 =
=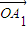 +¶À
+¶À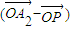 £ª
£ª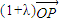 =
=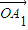 +¶À
+¶À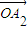 £¨º¥
£¨º¥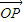 =
=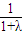
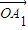 +
+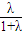
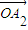 £ª
£ª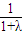 £¨a2=
£¨a2=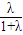 £¨‘Ú”–a1+a2=1£Æ
£¨‘Ú”–a1+a2=1£Æ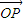 =a1
=a1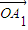 +a2
+a2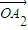 +°≠+an
+°≠+an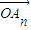 £¨
£¨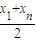 £¨Õ¨¿Ìy=
£¨Õ¨¿Ìy=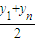 £¨«“µ„P
£¨«“µ„P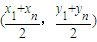 ‘⁄÷±œþl…œ£® «A1°¢Anµƒ÷–µ„£©£¨
‘⁄÷±œþl…œ£® «A1°¢Anµƒ÷–µ„£©£¨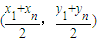 ¬˙◊„“™«Û£Æ
¬˙◊„“™«Û£Æ

 «·À…øŒÃ√µ•‘™∆⁄÷–∆⁄ƒ©◊®Ã‚≥Â¥Ã100∑÷œµ¡–¥∞∏
«·À…øŒÃ√µ•‘™∆⁄÷–∆⁄ƒ©◊®Ã‚≥Â¥Ã100∑÷œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| x2 |
| k-1 |
| y2 |
| k-3 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| n(n+1)(n+2) |
| 6 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 3 |
| 3 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
|
| 2 |
| 3¶– |
| 4 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
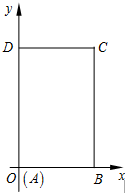 »ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨“—÷™æÿ–ŒABCDµƒ¡Ω±þAB£¨CD∑÷±¬‰‘⁄x÷·°¢y÷·µƒ’˝∞Î÷·…œ£¨«“AB=2£¨AD=4£¨µ„A”Î◊¯±Í‘≠µ„÷ÿ∫œ£Æœ÷Ω´æÿ–Œ’€µ˛£¨ πµ„A¬‰‘⁄œþ∂ŒDC…œ£¨»Ù’€∫€À˘‘⁄µƒ÷±œþµƒ–±¬ Œ™k£¨ ‘–¥≥ˆ’€∫€À˘‘⁄÷±œþµƒ∑Ω≥ú∞kµƒ∑∂Œß£Æ
»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨“—÷™æÿ–ŒABCDµƒ¡Ω±þAB£¨CD∑÷±¬‰‘⁄x÷·°¢y÷·µƒ’˝∞Î÷·…œ£¨«“AB=2£¨AD=4£¨µ„A”Î◊¯±Í‘≠µ„÷ÿ∫œ£Æœ÷Ω´æÿ–Œ’€µ˛£¨ πµ„A¬‰‘⁄œþ∂ŒDC…œ£¨»Ù’€∫€À˘‘⁄µƒ÷±œþµƒ–±¬ Œ™k£¨ ‘–¥≥ˆ’€∫€À˘‘⁄÷±œþµƒ∑Ω≥ú∞kµƒ∑∂Œß£Æ≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com