
【题目】某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如如图所示的部分频率分布直方图,请观察图形信息,回答下列问题: 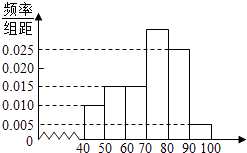
(1)求70~80分数段的学生人数;
(2)估计这次考试中该学科的优分率(80分及以上为优分)、中位数、平均值;
(3)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组、…、第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差大于30分(以分数段为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
【答案】
(1)解:根据题意得:60×[1﹣(0.005+0.010+0.015×2+0.025)×10]=18(人)
(2)解:成绩在80分及以上的学生有60×(0.005+0.025)×10=18(人),
∴估计这次考试中该学科的优分率为 ![]() ×100%=30%;
×100%=30%;
该学科40~50分数段人数为60×0.01×10=6(人);50~60分数段人数为60×0.015×10=9(人);60~70分数段人数为60×0.015×10=9(人);
70~80分数段人数为18人;80~90分数段人数为60×0.025×10=15(人);90~100分数段人数为60×0.005×10=3(人);
∴估计这次考试中位数为70~80分数段,即75分;
平均值为 ![]() (45×6+55×9+65×9+75×18+85×15+95×3)=71(分)
(45×6+55×9+65×9+75×18+85×15+95×3)=71(分)
(3)解:所有的组合数:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),即n=5+4+3+2+1=15,
符合“最佳组合”条件的有:(1,4),(1,5),(1,6),(2,5),(2,6),(3,6),即m=6,
则P= ![]() =
= ![]() =
= ![]()
【解析】(1)根据条形统计图1求出70~80分数段的学生人数频率,乘以60即可确定出人数;(2)求出80分及以上学生人数,确定出优生率,找出中位数,平均值即可;(3)根据题意得出所有等可能的情况数,找出“最佳组合”数,即可确定出选出的两组为“最佳组合”的概率.


科目:高中数学 来源: 题型:
【题目】(12分)已知椭圆C:![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1,![]() ),P4(1,
),P4(1,![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点P(m,n)的直线l与直线l0:x+2y+4=0垂直. (Ⅰ)若 ![]() ,且点P在函数
,且点P在函数 ![]() 的图像上,求直线l的一般式方程;
的图像上,求直线l的一般式方程;
(Ⅱ)若点P(m,n)在直线l0上,判断直线mx+(n﹣1)y+n+5=0是否经过定点?若是,求出该定点的坐标;否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张先生知道清晨从甲地到乙地有好、中、差三个班次的客车.但不知道具体谁先谁后.他打算:第一辆看后一定不坐,若第二辆比第一辆舒服,则乘第二辆;否则坐第三辆.问张先生坐到好车的概率和坐到差车的概率分别是( )
A.![]() 、
、 ![]()
B.![]() 、
、 ![]()
C.![]() 、
、 ![]()
D.![]() 、
、 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=f(x)﹣a
,g(x)=f(x)﹣a
(1)当a=2时,求函数g(x)的零点;
(2)若函数g(x)有四个零点,求a的取值范围;
(3)在(2)的条件下,记g(x)得四个零点分别为x1 , x2 , x3 , x4 , 求x1+x2+x3+x4的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元;未售出的产品,每盒亏损
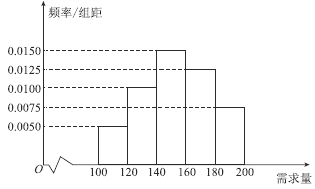
元;未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的首项a1= ![]() ,公比q满足q>0且q≠1,又已知a1 , 5a3 , 9a5成等差数列;
,公比q满足q>0且q≠1,又已知a1 , 5a3 , 9a5成等差数列;
(1)求数列{an}的通项公式;
(2)令bn=log3 ![]() ,记Tn=
,记Tn= ![]() ,是否存在最大的整数m,使得对任意n∈N* , 均有Tn>
,是否存在最大的整数m,使得对任意n∈N* , 均有Tn> ![]() 成立?若存在,求出m,若不存在,请说明理由.
成立?若存在,求出m,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com