
【题目】若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,且
两点,且![]() 关于直线
关于直线![]() 对称,动点P
对称,动点P![]() 在不等式组
在不等式组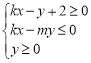 表示的平面区域内部及边界上运动,则
表示的平面区域内部及边界上运动,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】若p,q为简单命题,则“p且q为假”是“p或q为假”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() 算得,
算得,![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人坐飞机去外地办一件急事,下面是他自己从家里出发到坐在机舱内这一过程的主要算法:
S1 乘车去飞机场售票处;
S2 _____;
S3 凭票上机,对号入座.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定函数![]() ,若对于定义域中的任意
,若对于定义域中的任意![]() ,都有
,都有![]() 恒成立,则称函数
恒成立,则称函数![]() 为“爬坡函数”.
为“爬坡函数”.
(1)证明:函数![]() 是爬坡函数;
是爬坡函数;
(2)若函数![]() 是爬坡函数,求实数m的取值范围;
是爬坡函数,求实数m的取值范围;
(3)若对任意的实数b,函数![]() 都不是爬坡函数,求实数c的取值范围.
都不是爬坡函数,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某加工厂用某原料由车间加工出 产品,由乙车间加工出 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克 产品,每千克 产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克 产品,每千克 产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
A. 甲车间加工原料10箱,乙车间加工原料60箱
B. 甲车间加工原料15箱,乙车间加工原料55箱
C. 甲车间加工原料18箱,乙车间加工原料50箱
D. 甲车间加工原料40箱,乙车间加工原料30箱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若pVq是假命题,则( )
A. p,q至少有一个是假命题 B. p,q 均为假命题
C. p,q中恰有一个是假命题 D. p,q至少有一个是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com