
���� ��1�����ö����¼��ĸ��ʼ���ò�Ʒ�������۵ĸ���ֵ��
��2��������֪X�Ŀ���ȡֵΪ-320��-200��-80��40��160�������Ӧ�ĸ���ֵ��д���ֲ��У�������ѧ����E��X����
��� �⣺��1���ǡ��ò�Ʒ�������ۡ�Ϊ�¼�A��
��P��A��=1-��1-$\frac{1}{6}$������1-$\frac{1}{10}$��=$\frac{1}{4}$��
���ԣ��ò�Ʒ�������۵ĸ���Ϊ$\frac{1}{4}$����4�֣�
��2������֪��X�Ŀ���ȡֵΪ-320��-200��-80��40��160����5�֣�
����P��X=-320��=${��\frac{1}{4}��}^{4}$=$\frac{1}{256}$��
P��X=-200��=${C}_{4}^{1}$•${��\frac{1}{4}��}^{3}$•$\frac{3}{4}$=$\frac{3}{64}$��
P��X=-80��=${C}_{4}^{2}$•${��\frac{1}{4}��}^{2}$•${��\frac{3}{4}��}^{2}$=$\frac{27}{128}$��
P��X=40��=${C}_{4}^{3}$•$\frac{1}{4}$•${��\frac{3}{4}��}^{3}$=$\frac{27}{64}$��
P��X=160��=${��\frac{3}{4}��}^{4}$=$\frac{81}{256}$����10�֣�
����X�ķֲ���Ϊ
| X | -320 | -200 | -80 | 40 | 160 |
| P | $\frac{1}{256}$ | $\frac{3}{64}$ | $\frac{27}{128}$ | $\frac{27}{64}$ | $\frac{81}{256}$ |
���� ���⿼������ɢ����������ķֲ�������ѧ������Ӧ�����⣬�ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
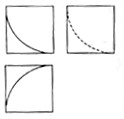 ��ͼ��ʾ��ij�����������ͼ�������߳�Ϊ1�������μ�ÿ����������һ�ΰ뾶Ϊ1��Բ�Ľ�Ϊ90���Բ������ü����������ǣ�������
��ͼ��ʾ��ij�����������ͼ�������߳�Ϊ1�������μ�ÿ����������һ�ΰ뾶Ϊ1��Բ�Ľ�Ϊ90���Բ������ü����������ǣ�������| A�� | 1-$\frac{��}{12}$ | B�� | 1-$\frac{��}{3}$ | C�� | 1-$\frac{��}{6}$ | D�� | 1-$\frac{��}{24}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | $\frac{5}{8}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com