
【题目】某健身馆为响应十九届四中全会提出的“聚焦增强人民体质,健全促进全民健身制度性举措”,提高广大市民对全民健身运动的参与程度,推出了让健身馆会员参与的健身促销活动.
(1)为了解会员对促销活动的兴趣程度,现从某周六参加该健身馆健身活动的会员中随机采访男性会员和女性会员各![]() 人,他们对于此次健身馆健身促销活动感兴趣的程度如下表所示:
人,他们对于此次健身馆健身促销活动感兴趣的程度如下表所示:
感兴趣 | 无所谓 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
根据以上数据能否有![]() 的把握认为“对健身促销活动感兴趣”与“性别”有关?
的把握认为“对健身促销活动感兴趣”与“性别”有关?
(参考公式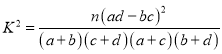 ,其中
,其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
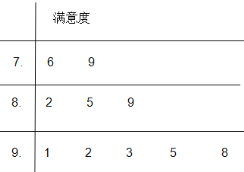
(2)在感兴趣的会员中随机抽取![]() 人对此次健身促销活动的满意度进行调查,以茎叶图记录了他们对此次健身促销活动满意度的分数(满分
人对此次健身促销活动的满意度进行调查,以茎叶图记录了他们对此次健身促销活动满意度的分数(满分![]() 分),如图所示,若将此茎叶图中满意度分为“很满意”(分数不低于
分),如图所示,若将此茎叶图中满意度分为“很满意”(分数不低于![]() 分)、“满意”(分数不低于平均分且低于
分)、“满意”(分数不低于平均分且低于![]() 分)、“基本满意”(分数低于平均分)三个级别.先从“满意”和“很满意”的会员中随机抽取两人参加回访馈赠活动,求这两人中至少有一人是“很满意”会员的概率.
分)、“基本满意”(分数低于平均分)三个级别.先从“满意”和“很满意”的会员中随机抽取两人参加回访馈赠活动,求这两人中至少有一人是“很满意”会员的概率.
【答案】(1)没有![]() 的把握认为“健身促销活动感兴趣”与“性别”有关,理由见解析;(2)
的把握认为“健身促销活动感兴趣”与“性别”有关,理由见解析;(2)![]() .
.
【解析】
(1)计算![]() 的观测值,结合临界值表可得出结论;
的观测值,结合临界值表可得出结论;
(2)计算出这![]() 个数据的平均数,记这
个数据的平均数,记这![]() 人中“满意”的
人中“满意”的![]() 人分别为
人分别为![]() 、
、![]() 、
、![]() 、
、![]() ,“很满意”的
,“很满意”的![]() 人分别记为
人分别记为![]() 、
、![]() ,列举出所有的基本事件,并确定事件“这两人中至少有一人是“很满意”会员”所包含的基本事件,利用古典概型的概率公式可求得所求事件的概率.
,列举出所有的基本事件,并确定事件“这两人中至少有一人是“很满意”会员”所包含的基本事件,利用古典概型的概率公式可求得所求事件的概率.
解:(1)由列表可得:
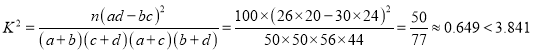 .
.
所以没有![]() 的把握认为“健身促销活动感兴趣”与“性别”有关;
的把握认为“健身促销活动感兴趣”与“性别”有关;
(2)由茎叶图知,这![]() 个数据的平均数为
个数据的平均数为![]() .
.
依题意这![]() 人中“满意”的有
人中“满意”的有![]() 人,记为
人,记为![]() 、
、![]() 、
、![]() 、
、![]() ,“很满意”的有
,“很满意”的有![]() 人,记为
人,记为![]() 、
、![]() .
.
从这![]() 人中任取
人中任取![]() 人,所有的基本事件有:
人,所有的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 个基本事件,
个基本事件,
记![]() 为从“满意”和“很满意”的会员中随机抽取两人至少有一人很满意,则
为从“满意”和“很满意”的会员中随机抽取两人至少有一人很满意,则![]() 中包含的基本事件有:
中包含的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 个基本事件.
个基本事件.
所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,分别过
有且仅有一个公共点,分别过![]() 两点作
两点作![]() ,垂足分别为
,垂足分别为![]() ,且记
,且记![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离, ![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,![]() 为点
为点![]() 到点
到点![]() 的距离,试探索
的距离,试探索![]() 是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 轴上方的点
轴上方的点![]() 在抛物线上,且
在抛物线上,且![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 与
与![]() 不重合),设直线
不重合),设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)当![]() 时,求证:直线
时,求证:直线![]() 恒过定点并求出该定点的坐标.
恒过定点并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.
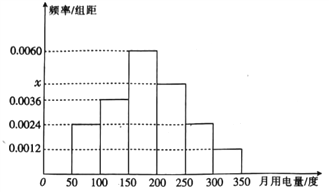
(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
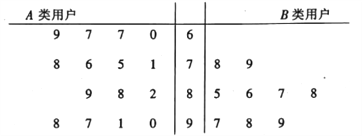
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| <>0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
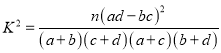 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 在
在![]() 轴上,
轴上,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,经过点
,经过点![]() 且垂直于
且垂直于![]() 轴的直线与抛物线
轴的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 到直线
到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右顶点,椭圆的右焦点为
的左、右顶点,椭圆的右焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值;
的值;
(2)设过点![]() 且斜率为1的直线与椭圆交于
且斜率为1的直线与椭圆交于![]() ,
,![]() (其中
(其中![]() ,
,![]() 分别在
分别在![]() 轴的上、下方)两点,当
轴的上、下方)两点,当![]() 时,记
时,记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的最小值,并求此时椭圆的标准方程.
的最小值,并求此时椭圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的不断发展和人们消费观念的不断提升,越来越多的人日益喜爱旅游观光.某人想在2019年5月到某景区![]() 旅游观光,为了避开旅游高峰拥挤,方便出行,他收集了最近5个月该景区的观光人数数据见下表:
旅游观光,为了避开旅游高峰拥挤,方便出行,他收集了最近5个月该景区的观光人数数据见下表:
月份 | 2018.12 | 2019.1 | 2019.2 | 2019.3 | 2019.4 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
旅游观光人数 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)由收集数据的散点图发现,可用线性回归模型拟合旅游观光人数少![]() (百万人)与月份编号
(百万人)与月份编号![]() 之间的相关关系,请用最小二乘法求
之间的相关关系,请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测2019年5月景区
,并预测2019年5月景区![]() 的旅游观光人数.
的旅游观光人数.
(2)当地旅游局为了预测景区![]() 给当地的财政带来的收入状况,从2019年4月的旅游观光人群中随机抽取了200人,并对他们旅游观光过程中的开支情况进行了调查,得到如下频率分布表:
给当地的财政带来的收入状况,从2019年4月的旅游观光人群中随机抽取了200人,并对他们旅游观光过程中的开支情况进行了调查,得到如下频率分布表:
开支金额(千元) |
|
|
|
|
|
|
|
频数 | 10 | 30 | 40 | 60 | 30 | 20 | 10 |
若采用分层抽样的方法从开支金额低于4千元的游客中抽取8人,再在这8人中抽取3人,记这3人中开支金额低于3千元的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(参考公式:![]() ,其中
,其中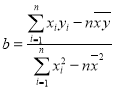 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,直线
,直线![]() 过
过![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.![]() 到准线的距离之和最小为8.
到准线的距离之和最小为8.
(1)求抛物线方程;
(2)若抛物线上一点![]() 纵坐标为
纵坐标为![]() ,直线
,直线![]() 分别交准线于
分别交准线于![]() .求证:以
.求证:以![]() 为直径的圆过焦点
为直径的圆过焦点![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com