
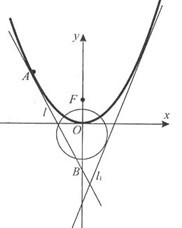
 (本题满分15分)如图,已知直线
(本题满分15分)如图,已知直线![]() 与抛物线
与抛物线![]() 和圆
和圆![]() 都相切,
都相切,![]() 是
是![]() 的焦点.
的焦点.
(1)求![]() 与
与![]() 的值;
的值;
(2)设![]() 是
是![]() 上的一动点,以
上的一动点,以![]() 为切点作抛物线
为切点作抛物线![]() 的切线
的切线![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,证明:点
,证明:点![]() 在一条定直线上;
在一条定直线上;
(3)在(2)的条件下,记点![]() 所在的定直线为
所在的定直线为![]() ,直线
,直线![]() 与
与![]() 轴交点为
轴交点为![]() ,连接
,连接![]() 交抛物线
交抛物线![]() 于
于![]() 两点,求
两点,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
22。(本题满分15分)已知函数![]() .
.
(1)求函数![]() 的图像在点
的图像在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,且
,且![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的最大值;
的最大值;
(3)当![]() 时,证明
时,证明![]() .
.
答案
22.(1)解:因为![]() ,所以
,所以![]() ,
,
函数![]() 的图像在点
的图像在点![]() 处的切线方程
处的切线方程![]() ;…………3分
;…………3分
(2)解:由(1)知,![]() ,所以
,所以![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立.…………4分
恒成立.…………4分
令![]() ,则
,则![]() ,……………………4分
,……………………4分
令![]()
![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上单调递增.………………………5分
上单调递增.………………………5分
因为![]() ,所以方程
,所以方程![]() 在
在![]() 上存在唯一实根
上存在唯一实根![]() ,且满足
,且满足![]() .
.
当![]() ,即
,即![]() ,当
,当![]() ,即
,即![]() ,…6分
,…6分
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() .…………7分
.…………7分
所以![]() .故整数
.故整数![]() 的最大值是3.………………………8分
的最大值是3.………………………8分
(3)由(2)知,![]() 是
是![]() 上的增函数,……………9分
上的增函数,……………9分
所以当![]() 时,
时,![]() .…………………10分
.…………………10分
即![]() .
.
整理,得![]() .………………11分
.………………11分
因为![]() , 所以
, 所以![]() .…………………12分
.…………………12分
即![]() .即
.即![]() .………………13分
.………………13分
所以![]() .………………………14分
.………………………14分


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
|
设![]() 的夹角为
的夹角为![]()
的取值范围; (III)设以点N(0,m)为圆心,以![]() 为
为
半径的圆与曲线E在第一象限的交点H,若圆在点H处的
切线与曲线E在点H处的切线互相垂直,求实数m的值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州八校高三9月期初联考文科数学试卷(解析版) 题型:解答题
(本题满分15分)如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, 与平面
与平面 所成角的正切值依次是
所成角的正切值依次是 和
和 ,
, ,
, 依次是
依次是 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三寒假作业数学卷三 题型:解答题
(本题满分15分)如图,在矩形ABCD中,点E,F分别在线段AB,AD上,AE=EB=AF= 沿直线EF将
沿直线EF将 翻折成
翻折成 使平面
使平面 平面BEF.
平面BEF.
(I)求二面角 的余弦值;
的余弦值;
(II)点M,N分别在线段FD,BC上,若沿直线MN将四边形MNCD向上翻折,使C
与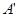 重合,求线段FM的长.
重合,求线段FM的长.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三年级随堂练习数学试卷 题型:解答题
(本题满分15分)
如图:某污水处理厂要在一个矩形污水处理池 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道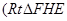 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 是
是 的中点,
的中点, 分别落在线段
分别落在线段 上.已知
上.已知 米,
米, 米,记
米,记 .
.
(Ⅰ)试将污水净化管道的长度 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
(Ⅱ)问:当 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度.

查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(浙江卷)理科数学 题型:解答题
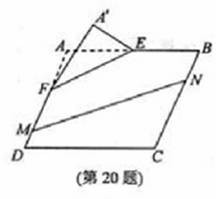 本题满分15分)如图, 在矩形
本题满分15分)如图, 在矩形 中,点
中,点 分别
分别
在线段 上,
上, .沿直线
.沿直线
将  翻折成
翻折成 ,使平面
,使平面 .
.
(Ⅰ)求二面角 的余弦值;
的余弦值;
(Ⅱ)点 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四
将四
边形 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段
的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com