
【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为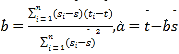 ,(说明:
,(说明:![]() 的导函数为
的导函数为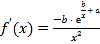 )
)
【答案】(1)选择![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;(3)20千万
;(3)20千万
【解析】
(1)由图可知![]() 适宜作为年产能
适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型;
的回归方程类型;
(2)由![]() ,得
,得![]() ,再利用最小二乘法求出
,再利用最小二乘法求出![]() ,从而得到
,从而得到![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)利用导数求得当![]() 时,
时,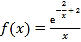 取得最大值.
取得最大值.
(1)由图可知![]() 适宜作为年产能
适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型
的回归方程类型
![]() 若选择
若选择![]() ,则
,则![]() ,此时当
,此时当![]() 接近于0时,
接近于0时,![]() 必小于0,
必小于0,
故选择![]() 作为年产能
作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型
的回归方程类型
(2)由![]() ,得
,得![]() ,故
,故![]() 与
与![]() 符合线性回归,
符合线性回归,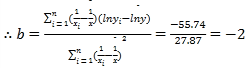 .
.
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 关于
关于![]() 的回归方程
的回归方程![]() .
.
(3)当人均产能达到最大时,年产能也达到最大,
由(2)可知人均产能函数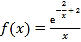 ,
,
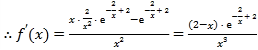 ,
,
![]() 时,
时,![]() ,
,![]() 时
时![]() ,
,
![]() 时,
时,![]() 单调递增,
单调递增,![]() 时,
时,![]() 单调递减,
单调递减,
![]() 当
当![]() 时,人均产能函数
时,人均产能函数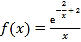 达到最大值,
达到最大值,
因此,每2千万资金安排2百人进行生产,能使人均产能达到最大,
![]() 对于该企业共有2000名生产工人,且资金充足,
对于该企业共有2000名生产工人,且资金充足,
![]() 下一年度应该投入20千万资金进行生产,可以适当企业的产能达到最大.
下一年度应该投入20千万资金进行生产,可以适当企业的产能达到最大.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函数f(x)的定义域;
(2)讨论函数f(x)的奇偶性;
(3)求a的取值范围,使f(x)>0在定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若不等式
,若不等式![]() 对一切
对一切![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(3)设数列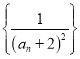 的前n项和为
的前n项和为![]() ,求证:对任意正整数n,都有
,求证:对任意正整数n,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是
列联表,已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.35.
地区当中“非常满意”的观众的概率为0.35.
非常满意 | 满意 | 合计 | |
| 30 | 15 | |
|
|
| |
合计 |
(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“非常满意”的![]() 、
、![]() 地区的人数各是多少.
地区的人数各是多少.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
(3)若以抽样调查的频率为概率,从![]() 地区随机抽取3人,设抽到的观众“非常满意”的人数为
地区随机抽取3人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ2﹣6ρcosθ+5=0,曲线C2的参数方程为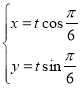 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程,并说明是什么曲线?
(2)若曲线C1与C2相交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个小商店从一家食品有限公司购进10袋白糖,每袋白糖的标准重量是500g,为了了解这些白糖的实际重量,称量出各袋白糖的实际重量(单位:g)如下:503,502,496,499,491,498,506,504,501,510
(1)求这10袋白糖的平均重量![]() 和标准差s;
和标准差s;
(2)从这10袋中任取2袋白糖,那么其中恰有一袋的重量不在(![]() s,
s,![]() s)的概率是多少?(附:
s)的概率是多少?(附:![]() 5.08,
5.08,![]() 16.06,
16.06,![]() 5.09,
5.09,![]() 16.09)
16.09)
查看答案和解析>>
科目:高中数学 来源: 题型:
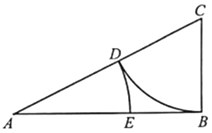
【题目】古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出己知线段的黄金分割点,具体方法如下:(l)取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=![]() AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:
AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:![]() 2.236)
2.236)
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的![]() 位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下图所示.
位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下图所示.

(Ⅰ)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(Ⅱ)若按分层抽样的方法从年龄在![]() 以内及
以内及![]() 以内的市民中随机抽取5人,再从这5人中随机抽取2人进行调研,求抽取的2人中,至多1人年龄在
以内的市民中随机抽取5人,再从这5人中随机抽取2人进行调研,求抽取的2人中,至多1人年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com