
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中 、
、 是过抛物线
是过抛物线 焦点
焦点 的两条弦,且其焦点
的两条弦,且其焦点 ,
, ,点
,点 为
为 轴上一点,记
轴上一点,记 ,其中
,其中 为锐角.
为锐角.

(1)求抛物线 方程;
方程;
(2)如果使“蝴蝶形图案”的面积最小,求 的大小?
的大小?
(1)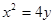 ;(2)
;(2)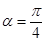 .
.
【解析】
试题分析:(1)抛物线焦点在 轴上,其标准方程为
轴上,其标准方程为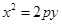 ,其中焦点坐标为
,其中焦点坐标为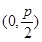 ;(2)显然要把蝴蝶形图案”的面积表示为
;(2)显然要把蝴蝶形图案”的面积表示为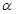 的函数,由于
的函数,由于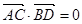 即
即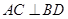 ,因此要求这个面积,只要求出
,因此要求这个面积,只要求出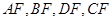 的长,当然它们都要用
的长,当然它们都要用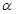 来表示,为此我们设
来表示,为此我们设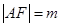 ,则
,则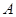 点坐标为
点坐标为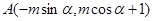 ,利用点
,利用点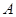 在抛物线
在抛物线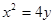 上,代入可得出关于
上,代入可得出关于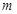 的二次方程,解方程求出
的二次方程,解方程求出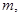 把
把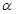 换成
换成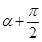 ,
,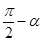 ,
,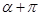 可依次得到
可依次得到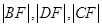 ,由此我们就可把面积
,由此我们就可把面积 用
用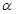 表示了,接下来只是涉及到求函数的最大值而已.
表示了,接下来只是涉及到求函数的最大值而已.
试题解析:(1)由抛物线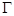 焦点
焦点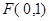 得,抛物线
得,抛物线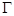 方程为
方程为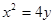
(2)设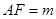 ,则点
,则点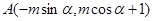
所以,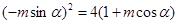 ,既
,既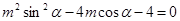
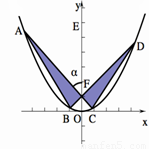
解得 
同理: 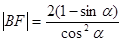
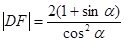
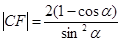
“蝴蝶形图案”的面积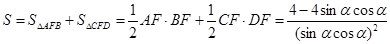
令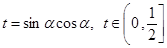 ,
, 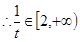
则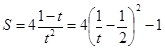 ,
, 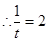 时,即
时,即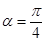 “蝴蝶形图案”的面积为8.
“蝴蝶形图案”的面积为8.
考点:(1)抛物线的标准方程;(2)圆锥曲线综合问题.


科目:高中数学 来源: 题型:
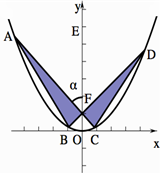 某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中AC、BD是过抛物线Γ焦点F的两条弦,且其焦点F(0,1),| AC |
| BD |
| 2(cosα+1) |
| sin2α |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海市杨浦区高三上学期学业质量调研文科数学试卷(解析版) 题型:解答题
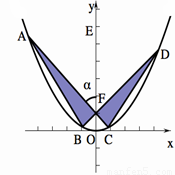
某校同学设计一个如图所示的“蝴蝶形图案(阴影区域)”,其中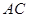 、
、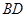 是过抛物线
是过抛物线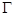 焦点
焦点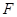 的两条弦,且其焦点
的两条弦,且其焦点 ,
,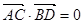 ,点
,点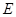 为
为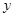 轴上一点,记
轴上一点,记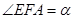 ,其中
,其中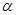 为锐角.
为锐角.
(1)求抛物线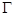 方程;
方程;
(2)求证: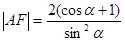 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com