
(本小题16分)
已知函数![]() 且
且![]()
(I)试用含![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)令![]() ,设函数
,设函数![]() 在
在![]() 处取得极值,记点
处取得极值,记点![]() ,证明:线段
,证明:线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() 、
、![]() 的公共点.
的公共点.
(本小题16分)
已知函数![]() 且
且![]()
(I)试用含![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅱ)求![]() 的单调区间;w.w.w.k.s.5.u.c.o.m
的单调区间;w.w.w.k.s.5.u.c.o.m
(Ⅲ)令![]() ,设函数
,设函数![]() 在
在![]() 处取得极值,记点
处取得极值,记点![]() ,证明:线段
,证明:线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() 、
、![]() 的公共点;
的公共点;
解法一:
![]()
![]()
依题意,得![]()
![]() ,--------------------------------------------------2分
,--------------------------------------------------2分
故![]() .------------------------------------------------------------------------------------4分
.------------------------------------------------------------------------------------4分
![]() 由
由![]() 得
得![]() ,
,
故![]() ,
,
令![]() ,则
,则![]() 或
或![]() ,--------------------------------------------------6分
,--------------------------------------------------6分
当![]() 时,
时, ![]() ,
,
当![]() 变化时,
变化时, ![]() 与
与 ![]() 的变化如下表:
的变化如下表:
|
| ( | ( | ( |
|
| + | - | + |
|
| 单调递增 | 单调递减 | 单调递增 |
由此得,函数![]() 的单调增区间为(
的单调增区间为(![]() ,
,![]() )和(
)和(![]() ,
, ![]() ),单调减区间为(
),单调减区间为(![]() ,
,![]() ).
).
当![]() 时,
时, ![]() .此时
.此时![]() 恒成立,且仅在
恒成立,且仅在![]() 处
处![]() ,故函数
,故函数![]() 的单调增区间为
的单调增区间为![]() .
.
当![]() 时,
时, ![]() ,同理可得函数
,同理可得函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() .--------------------------------------------------9分
.--------------------------------------------------9分
综上:当![]() 时,函数
时,函数![]() 的单调增区间为(
的单调增区间为(![]() ,
,![]() )和(
)和(![]() ,
, ![]() ),单调减区间为(
),单调减区间为(![]() ,
,![]() );当
);当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ; 当
; 当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() .-------------------------------10分
.-------------------------------10分
(Ⅲ)当![]() 时,得
时,得![]()
由![]() ,得
,得![]() ,
,![]() .
.
由(Ⅱ)得![]() 单调区间为
单调区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ,所以函数
,所以函数![]() 在
在![]() ,
,![]() 处取得极值;
处取得极值;
故![]() ,
,![]() .------------------------------------------------------------12分
.------------------------------------------------------------12分
所以直线![]() 的方程为
的方程为![]() ,
,
由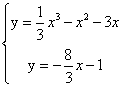 ,得
,得![]() -------------------------------14分
-------------------------------14分
令![]() .
.
易得![]() ,
,![]() .而
.而![]() 的图像在
的图像在![]() 内是一条连续不断的曲线,故
内是一条连续不断的曲线,故![]() 在
在![]() 内存在零点
内存在零点![]() ,这表明线段
,这表明线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() 、
、![]() 的公共点. --------------------------------------------------------------------------------------------------------------16分
的公共点. --------------------------------------------------------------------------------------------------------------16分
解法二:
(I)同解法一
(II)同解法一
(Ⅲ) 当![]() 时,得
时,得![]() ,由
,由![]() ,得
,得![]() ,
,![]() .
.
由(Ⅱ)得![]() 单调区间为
单调区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ,所以函数
,所以函数![]() 在
在![]() ,
,![]() 处取得极值;
处取得极值;
故![]() ,
,![]() .------------------------------------------------------------12分
.------------------------------------------------------------12分
所以直线![]() 的方程为
的方程为![]() ,
,
由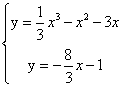 ,得
,得![]() -------------------------------14分
-------------------------------14分
解得:![]() ,
, ![]() ,
, ![]() .
.
∴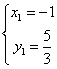 ,
, 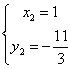 ,
, 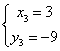 .
.
所以线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() 、
、![]() 的公共点
的公共点![]() .--------------16分
.--------------16分


科目:高中数学 来源:2010年江苏省扬州市高三第四次模拟考试数学试题 题型:解答题
(本小题16分)
已知抛物线的顶点在坐标原点,对称轴为 轴,焦点
轴,焦点 在直线
在直线 上,直线
上,直线 与抛物线相交于
与抛物线相交于 两点,
两点, 为抛物线上一动点(不同于
为抛物线上一动点(不同于 ),直线
),直线 分别交该抛物线的准线
分别交该抛物线的准线 于点
于点 。
。
(1)求抛物线方程;
(2)求证:以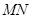 为直径的圆
为直径的圆 经过焦点
经过焦点 ,且当
,且当 为抛物线的顶点时,圆
为抛物线的顶点时,圆 与直线
与直线 相切。
相切。

查看答案和解析>>
科目:高中数学 来源:2010年江苏省高一第一学期期末测试数学试卷 题型:解答题
(本小题16分)
已知△OAB的顶点坐标为 ,
, ,
, , 点P的横坐标为14,且
, 点P的横坐标为14,且 ,点
,点 是边
是边 上一点,且
上一点,且 .
.
(1)求实数 的值与点
的值与点 的坐标;
的坐标;
(2)求点 的坐标;
的坐标;
(3)若 为线段
为线段 上的一个动点,试求
上的一个动点,试求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com