
ΓΨΧβΡΩΓΩΈΣΝΥΜΚΫβΫΜΆ®―ΙΝΠΘ§Ρ≥ Γ‘ΎΝΫΗω≥« –÷°ΦδΧΊ–ό“ΜΧθΉ®”ΟΧζ¬ΖΘ§”Ο“ΜΝ–Μπ≥ΒΉςΈΣΙΪΙ≤ΫΜΆ®≥ΒΘ°“―÷ΣΟΩ»’ά¥ΜΊΧΥ ΐy «ΟΩ¥ΈΆœΙ“≥ΒœαΫΎ ΐxΒΡ“Μ¥ΈΚ· ΐΘ§»γΙϊΗΟΝ–Μπ≥ΒΟΩ¥ΈΆœ4ΫΎ≥ΒœαΘ§ΟΩ»’Ρήά¥ΜΊ16ΧΥΘΜ»γΙϊΟΩ¥ΈΆœ6ΫΎ≥ΒœαΘ§‘ρΟΩ»’Ρήά¥ΜΊ10ΧΥΘ§Μπ≥ΒΟΩ»’ΟΩ¥ΈΆœΙ“≥ΒœαΒΡΫΎ ΐ «œύΆ§ΒΡΘ§ΟΩΫΎ≥Βœα¬ζ‘Ί ±Ρή‘ΊΩΆ110»ΥΘ°
Θ®1Θ©«σ≥ωyΙΊ”ΎxΒΡΚ· ΐΘΜ
Θ®2Θ©ΗΟΜπ≥Β¬ζ‘Ί ±ΟΩ¥ΈΆœΙ“Εύ…ΌΫΎ≥Βœα≤≈Ρή ΙΟΩ»’”Σ‘Υ»Υ ΐΉνΕύΘΩ≤Δ«σ≥ωΟΩΧλΉνΕύΒΡ”Σ‘Υ»Υ ΐΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©y=©¹3x+28Θ°Θ®2Θ©ΟΩ¥ΈΆœΙ“5ΫΎ≥Βœα≤≈Ρή ΙΟΩ»’”Σ‘Υ»Υ ΐΉνΕύΘ§ΉνΕύΒΡ”Σ‘Υ»Υ ΐΈΣ14300Θ°
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©…ηΟΩ»’ά¥ΜΊΧΥ ΐ![]() ”κΟΩ¥ΈΆœΙ“≥ΒœαΫΎ ΐ
”κΟΩ¥ΈΆœΙ“≥ΒœαΫΎ ΐ![]() ΒΡ“Μ¥ΈΚ· ΐΈΣ
ΒΡ“Μ¥ΈΚ· ΐΈΣ![]() .‘ρ”…“―÷ΣΩ…ΒΟΘ§ΗΟΚ· ΐΙΐΒψ
.‘ρ”…“―÷ΣΩ…ΒΟΘ§ΗΟΚ· ΐΙΐΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§¥ζ»κΚσΫβΒΟ
Θ§¥ζ»κΚσΫβΒΟ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΈΣ
ΒΡΚ· ΐΈΣ![]() ΘΜΘ®2Θ©”…Χβ“βΩ…÷ΣΟΩ»’”Σ‘Υ»Υ ΐ
ΘΜΘ®2Θ©”…Χβ“βΩ…÷ΣΟΩ»’”Σ‘Υ»Υ ΐ![]()
![]() Θ§“ρΈΣΕ‘≥Τ÷α
Θ§“ρΈΣΕ‘≥Τ÷α![]() Θ§Υυ“‘
Θ§Υυ“‘![]() .
.
‘ΧβΫβΈωΘΚΘ®1Θ©…η![]()
![]()
![]()
![]()
Θ®2Θ©…η![]() Θ§
Θ§ ![]()
![]()
ΓΏΕ‘≥Τ÷α![]() Θ§
Θ§
Γύ![]()
¥πΘΚΟΩ¥ΈΆœΙ“![]() ΫΎ≥Βœα≤≈Ρή ΙΟΩ»’”Σ‘Υ»Υ ΐΉνΕύΘ§ΉνΕύΒΡ”Σ‘Υ»Υ ΐΈΣ
ΫΎ≥Βœα≤≈Ρή ΙΟΩ»’”Σ‘Υ»Υ ΐΉνΕύΘ§ΉνΕύΒΡ”Σ‘Υ»Υ ΐΈΣ![]() .
.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Τσ“Β”–ΦΉΓΔ““ΝΫΗω―–ΖΔ–ΓΉιΘ§ΥϊΟ«―–ΖΔ–¬≤ζΤΖ≥…ΙΠΒΡΗ≈¬ Ζ÷±πΈΣ ![]() ΚΆ
ΚΆ ![]() Θ°œ÷Α≤≈≈ΦΉΉι―–ΖΔ–¬≤ζΤΖAΘ§““Ήι―–ΖΔ–¬≤ζΤΖBΘ§…ηΦΉΓΔ““ΝΫΉιΒΡ―–ΖΔœύΜΞΕάΝΔΘ°
Θ°œ÷Α≤≈≈ΦΉΉι―–ΖΔ–¬≤ζΤΖAΘ§““Ήι―–ΖΔ–¬≤ζΤΖBΘ§…ηΦΉΓΔ““ΝΫΉιΒΡ―–ΖΔœύΜΞΕάΝΔΘ°
Θ®ΔώΘ©«σ÷Ν…Ό”–“Μ÷÷–¬≤ζΤΖ―–ΖΔ≥…ΙΠΒΡΗ≈¬ ΘΜ
Θ®ΔρΘ©»τ–¬≤ζΤΖA―–ΖΔ≥…ΙΠΘ§‘ΛΦΤΤσ“ΒΩ…Μώάϊ»σ120Άρ‘ΣΘΜ»τ–¬≤ζΤΖB―–ΖΔ≥…ΙΠΘ§‘ΛΦΤΤσ“ΒΩ…Μώάϊ»σ100Άρ‘ΣΘ§«σΗΟΤσ“ΒΩ…Μώάϊ»σΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=Θ®3©¹aΘ©x©¹2+a©¹2lnxΘ®aΓ RΘ©
Θ®1Θ©»τΚ· ΐy=fΘ®xΘ©‘Ύ«χΦδΘ®1Θ§3Θ©…œΒΞΒςΘ§«σaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τΚ· ΐgΘ®xΘ©=fΘ®xΘ©©¹x‘ΎΘ®0Θ§ ![]() Θ©…œΈόΝψΒψΘ§«σaΒΡΉν–Γ÷ΒΘ°
Θ©…œΈόΝψΒψΘ§«σaΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() ΚΆΕ®Βψ
ΚΆΕ®Βψ![]() Θ§”…
Θ§”…![]() Άβ“ΜΒψ
Άβ“ΜΒψ![]() œρ
œρ![]() “ΐ«–œΏ
“ΐ«–œΏ![]() Θ§«–ΒψΈΣ
Θ§«–ΒψΈΣ![]() Θ§«“¬ζΉψ
Θ§«“¬ζΉψ![]() .Θ®1Θ©«σ Β ΐ
.Θ®1Θ©«σ Β ΐ![]() Φδ¬ζΉψΒΡΒ»ΝΩΙΊœΒΘΜ
Φδ¬ζΉψΒΡΒ»ΝΩΙΊœΒΘΜ
Θ®2Θ©«σœΏΕΈ![]() ≥ΛΒΡΉν–Γ÷ΒΘΜ
≥ΛΒΡΉν–Γ÷ΒΘΜ
Θ®3Θ©»τ“‘![]() ΈΣ‘≤–ΡΥυΉςΒΡ
ΈΣ‘≤–ΡΥυΉςΒΡ![]() ”κ
”κ![]() ”–ΙΪΙ≤ΒψΘ§ ‘«σΑκΨΕ»ΓΉν–Γ÷Β ±ΒΡ
”–ΙΪΙ≤ΒψΘ§ ‘«σΑκΨΕ»ΓΉν–Γ÷Β ±ΒΡ![]() ΖΫ≥Χ.
ΖΫ≥Χ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=log4Θ®4x+1Θ©+kx”κgΘ®xΘ©=log4Θ®a2x©¹![]() aΘ©Θ§Τδ÷–fΘ®xΘ© «≈ΦΚ· ΐΘ°
aΘ©Θ§Τδ÷–fΘ®xΘ© «≈ΦΚ· ΐΘ°
Θ®1Θ©«σ Β ΐkΒΡ÷ΒΘΜ
Θ®2Θ©«σΚ· ΐgΘ®xΘ©ΒΡΕ®“ε”ρΘΜ
(3)»τΚ· ΐfΘ®xΘ©”κgΘ®xΘ©ΒΡΆΦœσ”–«“÷Μ”–“ΜΗωΙΪΙ≤ΒψΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§Θ®
Θ§Θ® ![]() Θ© «≈ΦΚ· ΐΘ°
Θ© «≈ΦΚ· ΐΘ°
Θ®1Θ©«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©…ηΚ· ΐ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ°»τΚ· ΐ
Θ°»τΚ· ΐ![]() ”κ
”κ![]() ΒΡΆΦœσ”–«“÷Μ”–“ΜΗωΫΜΒψΘ§«σ
ΒΡΆΦœσ”–«“÷Μ”–“ΜΗωΫΜΒψΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥ‘ΛΖάΦΉ–Ά![]() ΝςΗ–,Ρ≥―ß–ΘΕ‘ΫΧ “≤…”Ο“©―§œϊΕΨΖ®Ϋχ––œϊΕΨ,“―÷Σ“©Έο»Φ…’ ± “ΡΎΟΩΝΔΖΫΟΉΩ’Τχ÷–ΒΡΚ§“©ΝΩ
ΝςΗ–,Ρ≥―ß–ΘΕ‘ΫΧ “≤…”Ο“©―§œϊΕΨΖ®Ϋχ––œϊΕΨ,“―÷Σ“©Έο»Φ…’ ± “ΡΎΟΩΝΔΖΫΟΉΩ’Τχ÷–ΒΡΚ§“©ΝΩ![]() ”κ ±Φδ
”κ ±Φδ![]() ≥…’ΐ±»άΐ,“©Έο»Φ…’ΆξΚσ¬ζΉψ
≥…’ΐ±»άΐ,“©Έο»Φ…’ΆξΚσ¬ζΉψ![]() ,»γΆΦΥυ Ψ,œ÷≤βΒΟ“©Έο8
,»γΆΦΥυ Ψ,œ÷≤βΒΟ“©Έο8![]() »Φ±œ,¥Υ ± “ΡΎΩ’Τχ÷–ΟΩΝΔΖΫΟΉΒΡΚ§“©ΝΩΈΣ6
»Φ±œ,¥Υ ± “ΡΎΩ’Τχ÷–ΟΩΝΔΖΫΟΉΒΡΚ§“©ΝΩΈΣ6![]() ,«κΑ¥Χβ÷–ΥυΙ©ΗχΒΡ–≈œΔ,Ϋβ¥πœ¬Ν–ΗςΧβ.
,«κΑ¥Χβ÷–ΥυΙ©ΗχΒΡ–≈œΔ,Ϋβ¥πœ¬Ν–ΗςΧβ.
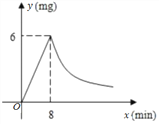
(1)«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΫβΈω Ϋ;
ΒΡΚ· ΐΫβΈω Ϋ;
(2)―–ΨΩ±μΟς,Β±Ω’Τχ÷–ΟΩΝΔΖΫΟΉΒΡΚ§“©ΝΩ≤ΜΒΆ”Ύ![]() «“≥÷–χ ±Φδ≤ΜΒΆ”Ύ
«“≥÷–χ ±Φδ≤ΜΒΆ”Ύ![]() ±≤≈Ρή”––ß…±ΟπΩ’Τχ÷–ΒΡ≤ΓΨζ,Ρ«Ο¥¥Υ¥ΈœϊΕΨ «Ζώ”––ß?ΈΣ ≤Ο¥?
±≤≈Ρή”––ß…±ΟπΩ’Τχ÷–ΒΡ≤ΓΨζ,Ρ«Ο¥¥Υ¥ΈœϊΕΨ «Ζώ”––ß?ΈΣ ≤Ο¥?
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΙφΕ®E={a1 Θ§ a2 Θ§ Γ≠Θ§a10}ΒΡΉ”Φ·{at1 Θ§ at2 Θ§ Γ≠Θ§ak}ΈΣEΒΡΒΎkΗωΉ”Φ·Θ§Τδ÷– ![]() Θ§‘ρEΒΡΒΎ211ΗωΉ”Φ· « Θ°
Θ§‘ρEΒΡΒΎ211ΗωΉ”Φ· « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΚ· ΐhΘ®xΘ©=ax3+bx2+cx+dΘ®aΓΌ0Θ©ΆΦœσΒΡΕ‘≥Τ÷––ΡΈΣMΘ®x0 Θ§ hΘ®x0Θ©Θ©Θ§Φ«Κ· ΐhΘ®xΘ©ΒΡΒΦΚ· ΐΈΣgΘ®xΘ©Θ§‘ρ”–gΓδΘ®x0Θ©=0Θ§…ηΚ· ΐfΘ®xΘ©=x3©¹3x2+2Θ§‘ρfΘ® ![]() Θ©+fΘ®
Θ©+fΘ® ![]() Θ©+Γ≠+fΘ®
Θ©+Γ≠+fΘ® ![]() Θ©+fΘ®
Θ©+fΘ® ![]() Θ©= Θ°
Θ©= Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com