
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的方程为
的方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 上有3个点到曲线
上有3个点到曲线![]() 的距离等于1,求
的距离等于1,求![]() 的值.
的值.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】据某市地产数据研究的数据显示,2016年该市新建住宅销售均价走势如下图所示,为抑制房价过快上涨,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.
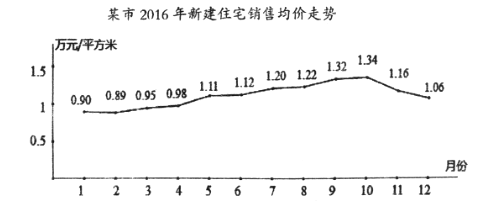
(1)地产数据研究院发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试建立
之间具有较强的线性相关关系,试建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
(2)地产数据研究院在2016年的12个月份中,随机抽取三个月的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据: ![]() ,
, ![]() ,
, ![]() ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
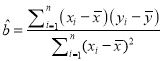 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某商业公司为全面激发每一位职工工作的积极性、创造性,确保2017年超额完成销售任务,向党的十九大献礼.年初该公司制定了一个激励销售人员的奖励方案:每季度销售利润不超过15万元时,则按其销售利润的![]() 进行奖励;当季销售利润超过15万元时,若超过部分为
进行奖励;当季销售利润超过15万元时,若超过部分为![]() 万元,则超出部分按
万元,则超出部分按![]() 进行奖励,没超出部分仍按季销售利润的
进行奖励,没超出部分仍按季销售利润的![]() 进行奖励.记奖金总额为
进行奖励.记奖金总额为![]() (单位:万元),季销售利润为
(单位:万元),季销售利润为![]() (单位:万元).
(单位:万元).
(Ⅰ)请写出该公司激励销售人员的奖励方案的函数表达式;
(Ⅱ)如果业务员李明在本年的第三季度获得5.5万元的奖金,那么,他在该季度的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关,在市第一人民医院随机对入院50人进行了问卷调查,得到了如表的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 5 | ||
女 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为患心肺疾病与性别有关?说明你的理由.
参考格式: 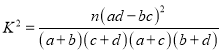 ,其中
,其中![]() .
.
下面的临界值仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一
人答一份).现从回收的年龄在20~60岁的问卷中随机抽取了100份,统计结果如下面的图表所示.
年龄 分组 | 抽取份数 | 答对全卷 的人数 | 答对全卷的人数 占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) |
| 27 | 0.9 |
[40,50) | 10 | 4 |
|
[50,60] | 20 |
| 0.1 |

(1)分别求出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)从年龄在![]() 答对全卷的人中随机抽取2人授予“环保之星”,求年龄在
答对全卷的人中随机抽取2人授予“环保之星”,求年龄在![]() 的人中至少有1人被授予“环保之星”的概率.
的人中至少有1人被授予“环保之星”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为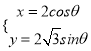 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,与直角坐标系
轴的正半轴为极轴,与直角坐标系![]() 取相同的单位长度建立极坐标系,曲线
取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)化曲线![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线![]() 与
与![]() 轴的一个交点的坐标为
轴的一个交点的坐标为![]() ,经过点
,经过点![]() 作斜率为1的直线,
作斜率为1的直线, ![]() 交曲线
交曲线![]() 于
于![]() 两点,求线段
两点,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com