
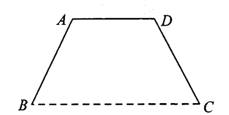
【题目】某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门![]() (如图).设计要求彩门的面积为
(如图).设计要求彩门的面积为![]() (单位:
(单位:![]() ),高为
),高为![]() (单位:
(单位:![]() )(
)(![]() 为常数).彩门的下底
为常数).彩门的下底![]() 固定在广场底面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为
固定在广场底面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为![]() ,不锈钢支架的长度和记为
,不锈钢支架的长度和记为![]() .
.
(1)请将![]() 表示成关于
表示成关于![]() 的函数
的函数![]() ;
;
(2)问当![]() 为何值
为何值![]() 最小,并求最小值.
最小,并求最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() .计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
.计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M,GH的中点为N.

(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由).
(2)判断平面BEG与平面ACH的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线C1的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数,数列
为正整数,数列![]() 满足
满足![]() ,
,![]() ,设数列
,设数列![]() 满足
满足![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)若数列![]() 是等差数列,前
是等差数列,前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列给出的输入语句、输出语句和赋值语句:
(1)输出语句INPUT ![]() ,b,c
,b,c
(2)输入语句INPUT ![]() =3
=3
(3)赋值语句3=A
(4)赋值语句A=B=C
则其中正确的个数是( )
(A)0 (B)1 (C)2 (D)3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() 且
且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明:![]() <0.
<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com