考点:函数恒成立问题,函数零点的判定定理
专题:综合题,函数的性质及应用
分析:(1)f(2
x)>0恒成立?2
x+
-1>0(x≠0)恒成立?m>2
x(1-2
x)(x≠0)恒成立,构造函数g(x)=2
x(1-2
x)(x≠0),利用基本不等式(或配方法)可求得m的取值范围;
(2)当x>0时,由f(x)=x+
-1=0得:m=x(1-x)=-(x-
)
2+
;同理可得,当x<0时,m=x(1+x)=(x+
)
2-
,在在同一直角坐标系中作出函数y=m与函数y=|x|(x-1)的图象,借助图象即可求得函数f(x)零点的个数.
解答:
解:(1)f(2
x)>0恒成立?2
x+
-1>0(x≠0)恒成立?m>2
x(1-2
x)(x≠0)恒成立,
令g(x)=2
x(1-2
x)(x≠0),
则m>g(x)
max,
因为g(x)=2
x(1-2
x)≤(
)
2=
(当且仅当x=-1时取“=”),
∴g(x)
max=
,
∴m>
;
(2)当x>0时,由f(x)=x+
-1=0得:m=x(1-x)=-(x-
)
2+
,
当x<0时,由f(x)=-x+
-1=0得:m=x(1+x)=(x+
)
2-
,
在同一直角坐标系中作出函数y=m与函数y=|x|(x-1)的图象,
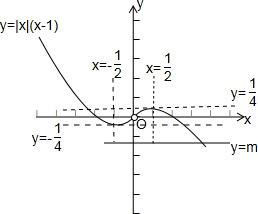
由图象知,当m<-
或m>
时,函数f(x)=|x|+
-1(x≠0)有一个零点;
当m=±
或m=0时,函数f(x)=|x|+
-1(x≠0)有两个零点;
当-
<m<0或0<m<
时,函数f(x)=|x|+
-1(x≠0)有三个零点.
点评:本题考查函数恒成立问题,考查函数零点的判定定理的应用,作图是关键,也是难点,着重考查等价转化思想与数形结合思想、分类讨论思想的综合运用,属于难题.




 智能训练练测考系列答案
智能训练练测考系列答案