
【题目】在矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,则在翻折过程中,异面直线
折起,则在翻折过程中,异面直线![]() 与
与![]() 所成角的取值范围是____.
所成角的取值范围是____.
【答案】![]()
【解析】
先由题意,取![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,得到
,得到![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,或所成角的补角,记异面直线
所成角,或所成角的补角,记异面直线![]() 与
与![]() 所成角为
所成角为![]() ,则
,则![]() ,根据题意,画出图形,结合翻折过程求出临界值,再由余弦定理,即可求出结果.
,根据题意,画出图形,结合翻折过程求出临界值,再由余弦定理,即可求出结果.
由题意,取![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
将![]() 沿
沿![]() 折起,在翻折过程中,始终有
折起,在翻折过程中,始终有![]() ,
,![]() ;
;
所以![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,或所成角的补角,
所成角,或所成角的补角,
记异面直线![]() 与
与![]() 所成角为
所成角为![]() ,则
,则![]()
因为![]() ,不放设
,不放设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
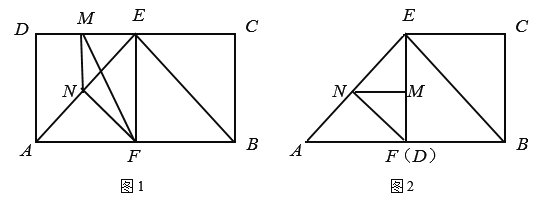
由题意可得,在翻折过程中,![]() 逐渐减小,当
逐渐减小,当![]() 点与
点与![]() 重合时,
重合时,![]() 最小,如图2;
最小,如图2;
此时![]() ;
;
翻折前,![]() 取最大,如图1;此时
取最大,如图1;此时![]() ,
,
所以![]() ,
,
由余弦定理可得:![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即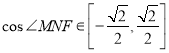 ,
,
所以 ,因此
,因此![]() ;
;
又翻折前,以及点![]() 点与
点与![]() 重合,这两种情况下,
重合,这两种情况下,![]() 与
与![]() 是相交直线,
是相交直线,
所以![]() ,即
,即![]() ;
;
故![]() .
.
故答案为:![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】设集合X是实数R的子集,如果点![]() 满足:对任意
满足:对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() ,那么称
,那么称![]() 为集合X的聚点.集合①
为集合X的聚点.集合①![]() ;②R除去
;②R除去![]() ;③
;③![]() ;④Z其中以0为聚点的集合有( ).
;④Z其中以0为聚点的集合有( ).
A.②③B.①④C.①③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).![]() 是曲线
是曲线![]() 上的动点,将线段
上的动点,将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到线段
得到线段![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(I)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(II)在(I)的条件下,若射线![]() 与曲线
与曲线![]() ,
,![]() 分别交于
分别交于![]() 两点(除极点外),且有定点
两点(除极点外),且有定点![]() ,求
,求![]() 面积.
面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王、小李在两次数学考试中答对题数如下表表示:
题型 答对 题数 姓名 | 期中考试 | 期末考试 | ||||
填空题 (每题3分) | 选择题 每题3分) | 解答题 (每题8分) | 填空题 (每题3分) | 选择题 每题3分) | 解答题 (每题8分) | |
小王 | 10 | 3 | 2 | 11 | 4 | 4 |
小李 | 9 | 5 | 3 | 7 | 3 | 3 |
(1)用矩阵表示小王和小李期中考试答对题数、期末考试答对题数、每种题型的分值;
(2)用矩阵运算表示他们在两次考试中各题型答对题总数;
(3)用矩阵计算小王、小李两次考试各题型平均答对题数;
(4)用矩阵计算他们期中、期末的成绩;
(5)如果期中考试成绩占40%,期末考试成绩占60%,用矩阵求两同学的总评成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(1)求![]() 与
与![]() 的极坐标方程;
的极坐标方程;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有Ⅳ人参加,现将所有参加者按年龄情况分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等七组,其频率分布直方图如图所示,已知
等七组,其频率分布直方图如图所示,已知![]() 这组的参加者是6人.
这组的参加者是6人.

(1)根据此频率分布直方图求该校参加秋季登山活动的教职工年龄的中位数;
(2)已知![]() 和
和![]() 这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率;
这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率;
(3)组织者从![]() 这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为
这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为![]() ,求
,求![]() 的分布列和均值.
的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() 的焦点坐标为
的焦点坐标为![]() ,点
,点![]() ,过点P作直线l交抛物线C于A,B两点,过A,B分别作抛物线C的切线,两切线交于点Q,则
,过点P作直线l交抛物线C于A,B两点,过A,B分别作抛物线C的切线,两切线交于点Q,则![]() 面积的最小值为( )
面积的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com