
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x12+ax1+b |
| 2 |
| x22+ax2+b |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| (x1-x2)2 |
| 4 |
| 1 |
| x |
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2x1•x2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| 1 |
| x1x2(x1+x2) |
| (x1-x2)2 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| -lnx1-lnx2 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
2
| ||
| x1+x2 |


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源:福建省四地六校2011-2012学年高一第一次月考数学试题 题型:022
若函数f(x)同时满足:①对于定义域上的任意x,恒有f(x)+f(-x)=0;②对于定义域上的任意x1,x2,当x1≠x2时,恒有![]() ,则称函数f(x)为“理想函数”.给出下列四个函数中:
,则称函数f(x)为“理想函数”.给出下列四个函数中:
(1)![]()
(2)f(x)=x2
(3)![]()
(4)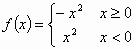 ,能被称为“理想函数”的有________(填相应的序号).
,能被称为“理想函数”的有________(填相应的序号).
查看答案和解析>>
科目:高中数学 来源:湖北省荆州中学2011-2012学年高一上学期期中考试数学(A)试题(人教版) 题型:022
若函数f(x)同时满足:
①对于定义域上的任意x,恒有f(x)+f(-x)=0
②对于定义域内任意x1,x2,当x1≠x2时,恒有![]() ,则称函数f(x)为“理想函数”.给出下列四个函数中:
,则称函数f(x)为“理想函数”.给出下列四个函数中:
(1)![]()
(2)f(x)=x2
(3)![]()
(4) ,能被称为“理想函数”的有________(填相应的序号).
,能被称为“理想函数”的有________(填相应的序号).
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市高三毕业班质量检查文科数学试卷(解析版) 题型:选择题
对于定义域为 的函数
的函数 ,若存在非零实数
,若存在非零实数 ,使函数
,使函数 在
在 和
和 上均有零点,则称
上均有零点,则称 为函数
为函数 的一个“界点”.则下列四个函数中,不存在“界点”的是
的一个“界点”.则下列四个函数中,不存在“界点”的是
A. B.
B.
C. D.
D.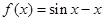
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com