
【题目】已知椭圆![]() +
+![]() =1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=
=1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=![]() (a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
(a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】现有一个以![]() 、
、![]() 为半径的扇形池塘,在
为半径的扇形池塘,在![]() 、
、![]() 上分别取点
上分别取点![]() 、
、![]() ,作
,作![]() 、
、![]() 分别交弧
分别交弧![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,现用渔网沿着
,现用渔网沿着![]() 、
、![]() 、
、![]() 、
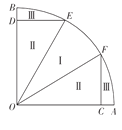
、![]() 将池塘分成如图所示的养殖区域.已知
将池塘分成如图所示的养殖区域.已知![]() ,
, ![]() ,
, ![]() (
(![]() ).
).
(1)若区域Ⅱ的总面积为![]() ,求
,求![]() 的值;
的值;
(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是30万元、40万元、20万元,试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据已往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为
(升),在水底作业10个单位时间,每单位时间用氧量为![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为
(米/单位时间),每单位时间用氧量为![]() (升),记该潜水员在此次考察活动中的总用氧量为
(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 过点
过点![]() ,且椭圆
,且椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若BA,求实数m的取值范围;
(2)当x∈R时,不存在元素x使x∈A与x∈B同时成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com