
【题目】设抛物线C:![]() 与直线
与直线![]() 交于A、B两点.
交于A、B两点.
(1)当![]() 取得最小值为
取得最小值为![]() 时,求
时,求![]() 的值.
的值.
(2)在(1)的条件下,过点![]() 作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且
作两条直线PM、PN分别交抛物线C于M、N(M、N不同于点P)两点,且![]() 的平分线与
的平分线与![]() 轴平行,求证:直线MN的斜率为定值.
轴平行,求证:直线MN的斜率为定值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
(1)求椭圆C的方程;
(2)设直线上![]() 与椭圆C交于A,B两点,点
与椭圆C交于A,B两点,点![]() ,且
,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自新型冠状病毒疫情爆发以来,人们时刻关注疫情,特别是治愈率,治愈率![]() 累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第
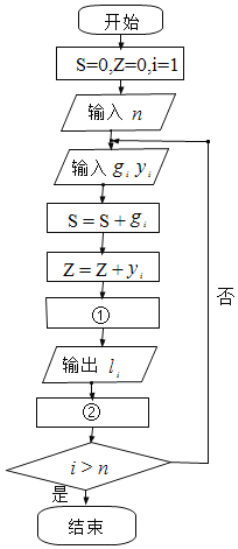
累计治愈人数/累计确诊人数,治愈率的高低是“战役”的重要数据,由于确诊和治愈人数在不断变化,那么人们就非常关心第![]() 天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
天的治愈率,以此与之前的治愈率比较,来推断在这次“战役”中是否有了更加有效的手段,下面是一段计算治愈率的程序框图,请同学们选出正确的选项,分别填入①②两处,完成程序框图.( )
![]() :第
:第![]() 天新增确诊人数;
天新增确诊人数;![]() :第
:第![]() 天新增治愈人数;
天新增治愈人数;![]() :第
:第![]() 天治愈率
天治愈率
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
①若![]() 在
在![]() 上是奇函数,则
上是奇函数,则![]() 在
在![]() 上也是奇函数
上也是奇函数
②若![]() 不是正弦函数,则
不是正弦函数,则![]() 不是周期函数
不是周期函数
③“若![]() ,则
,则![]() .”的否命题是“若
.”的否命题是“若![]() ,则
,则![]() .”
.”
④若![]() :
:![]() ;
;![]() :
:![]() ,则
,则![]() 是
是![]() 的充分不必要条件
的充分不必要条件
其中正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
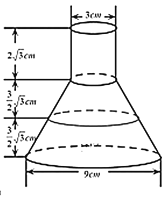
【题目】《乌鸦喝水》是《伊索寓言》中一个寓言故事,通过讲述已知乌鸦喝水的故事,告诉人们遇到困难要运用智慧,认真思考才能让问题迎刃而解的道理,如图![]() 所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为
所示,乌鸦想喝水,发现有一个锥形瓶,上面部分是圆柱体,下面部分是圆台,瓶口直径为![]() 厘米,瓶底直径为
厘米,瓶底直径为![]() 厘米,瓶口距瓶颈为
厘米,瓶口距瓶颈为![]() 厘米,瓶颈到水位线距离和水位线到瓶底距离均为
厘米,瓶颈到水位线距离和水位线到瓶底距离均为![]() 厘米,现将
厘米,现将![]() 颗石子投入瓶中,发现水位线上移
颗石子投入瓶中,发现水位线上移![]() 厘米,若只有当水位线到达瓶口时乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是( )
厘米,若只有当水位线到达瓶口时乌鸦才能喝到水,则乌鸦共需要投入的石子数量至少是( )
A.![]() 颗B.
颗B.![]() 颗C.
颗C.![]() 颗D.
颗D.![]() 颗
颗
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
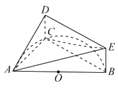
(1)证明:平面ADE⊥平面ACD;
(2)当C点为半圆的中点时,求二面角D﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:
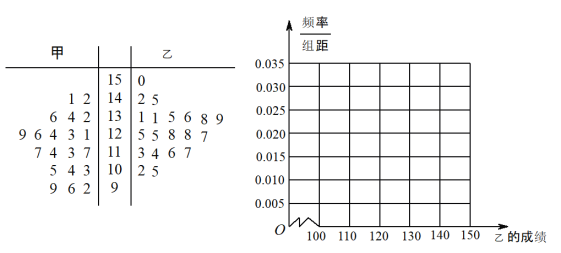
(1)根据茎叶图求甲乙两位同学成绩的中位数,并据此判断甲乙两位同学的成绩谁更好?
(2)将同学乙的成绩的频率分布直方图补充完整;
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设选出的2个成绩中含甲的成绩的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com