
【题目】已知a>1,f(x)=x2﹣ax , 当x∈(﹣1,1)时,均有f(x)< ![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.(1,2)
B.(1,3]
C.(1, ![]() )
)
D.(1,2]
科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本,(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出如下频率分布直方图.
的分组作出如下频率分布直方图.
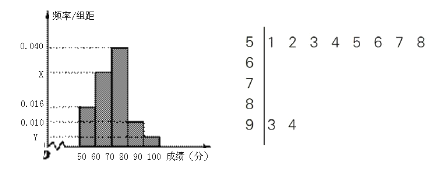
(1)由如下茎叶图(图中仅列出了得分在![]() ,
,![]() 的数据)提供的信息,求样本容量
的数据)提供的信息,求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,求所抽取的2名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个体户计划经销A、B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A、B商品中所获得的收益分别为f(x)万元与g(x)万元、其中f(x)=a(x﹣1)+2(a>0);g(x)=6ln(x+b),(b>0)已知投资额为零时,收益为零.
(1)试求出a、b的值;
(2)如果该个体户准备投入5万元经营这两种商品,请你帮他制定一个资金投入方案,使他能获得最大收益,并求出其收入的最大值.(精确到0.1,参考数据:ln3≈1.10).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的程序框图表示的算法中,输入三个实数a,b,c,要求输出的x是这三个数中最大的数,那么在空白的判断框中,应该填入( ) 
A.x>c
B.c>x
C.c>b
D.c>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a≥0,f(x)=x﹣1﹣ln2x+2alnx(x>0).
(1)令F(x)=xf′(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(2)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α是空间中的一个平面,l,m,n是三条不同的直线,则下列命题中正确的是( )
A.若mα,nα,l⊥m,l⊥n,则l⊥α
B.若mα,n⊥α,l⊥n,则l∥m
C.若l∥m,m⊥α,n⊥α,则l∥n
D.若l⊥m,l⊥n,则n∥m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆M:x2+y2﹣4x﹣2y+4=0
(1)若圆M的切线在x轴上的截距是y轴上的截距的2倍,求切线的方程;
(2)从圆外一点P(a,b),向该圆引切线PA,切点为A,且PA=PO,O为坐标原点,求证:以PM为直径的圆过异于M的定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为
(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为1.5(升),记潜水员在此次考察活动中的总用氧量为
(米/单位时间),每单位时间用氧量为1.5(升),记潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com