【答案】
分析:(1)设双曲线C的方程为
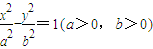
,由顶点坐标、渐近线方程及a、b、c 的关系求出a、b的值即得.
(2)设P(x
1,y
1),R(x
2,y
2),当直线l的斜率存在时,设设此直线方程为y=k(x+3),由
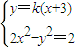
得(2-k
2)x
2-6k
2x-9k
2-2=0,再由方程的根与系数关系及
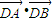
为定值;当直线l的斜率不存在时,当直线AB垂直于x轴时,其方程为x=-3,A,B的坐标为(-3,4)、(-3,-4),代入可求;
(3)对于过定点问题,可先假设存在,即假设直线MN过定点,再利用设直线MN的方程为:x=my+t,联立方程组,利用垂直关系求直线MN过定点,若出现矛盾,则说明假设不成立,即不存在;否则存在.最后运用类比推理写出类似结论.
解答:解:(1)设双曲线C的方程为
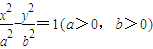
,则a=1,
又
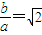
,得
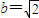
,所以,双曲线C的方程为
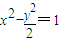
.
(2)当直线AB垂直于x轴时,其方程为x=-3,A,B的坐标为(-3,4)、(-3,-4),
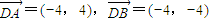
,得
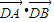
=0.
当直线AB不与x轴垂直时,设此直线方程为y=k(x+3),由
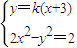
得(2-k
2)x
2-6k
2x-9k
2-2=0.
设A(x
1,y
1),B(x
2,y
2),则
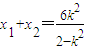
,
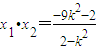
,
故
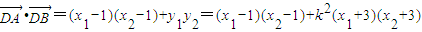
=
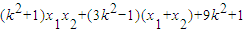
.
=
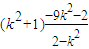
+
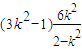
+9k
2+1=0.综上,
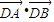
=0为定值.
(3)当M,N满足EM⊥EN时,取M,N关于x轴的对称点M'、N',由对称性知EM'⊥EN',此时MN与M'N'所在直线关于x轴对称,若直线MN过定点,则定点必在x轴上.
设直线MN的方程为:x=my+t,
由
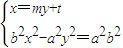
,得(b
2m
2-a
2)y
2+2b
2mty+b
2(t
2-a
2)=0
设M(x
1,y
1),N(x
2,y
2),则
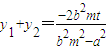
,
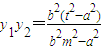
,
由EM⊥EN,得(x
1-a)(x
2-a)+y
1y
2=0,(my
1+t-a)(my
2+t-a)+y
1y
2=0,
即
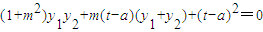
,
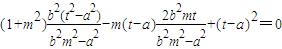
,
化简得,
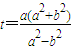
或t=a(舍),
所以,直线MN过定点(
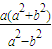
,0).
情形一:在双曲线Γ:
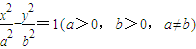
中,若E'为它的左顶点,M,N为双曲线Γ上的两点(都不同于点E'),且E'M⊥E'N,则直线MN过定点(
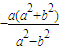
,0).
情形二:在抛物线y
2=2px(p>0)中,若M,N为抛物线上的两点(都不同于原点O),且OM⊥ON,则直线MN过定点(2p,0).…..(16分)
情形三:(1)在椭圆
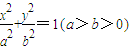
中,若E为它的右顶点,M,N为椭圆上的两点(都不同于点E),且EM⊥EN,则直线MN过定点(

,0);
(2)在椭圆
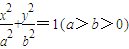
中,若E'为它的左顶点,M,N为椭圆上的两点(都不同于点E'),且E'M⊥E'N,则直线MN过定点(
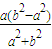
,0);
(3)在椭圆
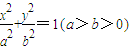
中,若F为它的上顶点,M,N为椭圆上的两点(都不同于点F),且FM⊥FN,则直线MN过定点(0,
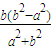
);
(4)在椭圆
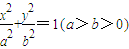
中,若F'为它的下顶点,M,N为椭圆上的两点(都不同于点F'),且F'M⊥F'N,则直线MN过定点(0,
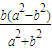
).
点评:本题主要考查了由双曲线的性质求解双曲线的方程,直线与双曲线的相交关系的应用,方程的根与系数关系的应用,向量的坐标表示的应用,属于直线与曲线位置关系的综合应用,属于综合性试题.

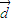 =
=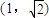 是它的一条渐近线的一个方向向量.
是它的一条渐近线的一个方向向量.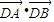 为定值;
为定值;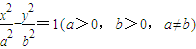 ,E为它的右顶点,M,N为双曲线Γ上的两点(都不同于点E),且EM⊥EN,那么直线MN是否过定点?若是,请求出此定点的坐标;若不是,说明理由.然后在以下三个情形中选择一个,写出类似结论(不要求书写求解或证明过程).
,E为它的右顶点,M,N为双曲线Γ上的两点(都不同于点E),且EM⊥EN,那么直线MN是否过定点?若是,请求出此定点的坐标;若不是,说明理由.然后在以下三个情形中选择一个,写出类似结论(不要求书写求解或证明过程).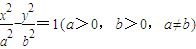 及它的左顶点;
及它的左顶点;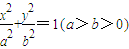 及它的顶点.
及它的顶点.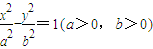 ,由顶点坐标、渐近线方程及a、b、c 的关系求出a、b的值即得.
,由顶点坐标、渐近线方程及a、b、c 的关系求出a、b的值即得.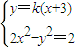 得(2-k2)x2-6k2x-9k2-2=0,再由方程的根与系数关系及
得(2-k2)x2-6k2x-9k2-2=0,再由方程的根与系数关系及 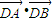 为定值;当直线l的斜率不存在时,当直线AB垂直于x轴时,其方程为x=-3,A,B的坐标为(-3,4)、(-3,-4),代入可求;
为定值;当直线l的斜率不存在时,当直线AB垂直于x轴时,其方程为x=-3,A,B的坐标为(-3,4)、(-3,-4),代入可求;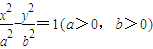 ,则a=1,
,则a=1,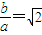 ,得
,得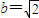 ,所以,双曲线C的方程为
,所以,双曲线C的方程为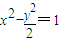 .
.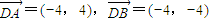 ,得
,得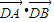 =0.
=0.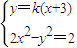 得(2-k2)x2-6k2x-9k2-2=0.
得(2-k2)x2-6k2x-9k2-2=0.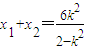 ,
,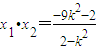 ,
,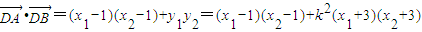
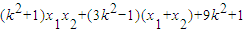 .
.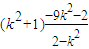 +
+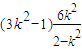 +9k2+1=0.综上,
+9k2+1=0.综上,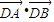 =0为定值.
=0为定值.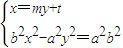 ,得(b2m2-a2)y2+2b2mty+b2(t2-a2)=0
,得(b2m2-a2)y2+2b2mty+b2(t2-a2)=0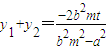 ,
,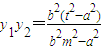 ,
,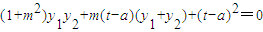 ,
,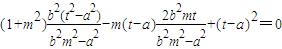 ,
,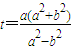 或t=a(舍),
或t=a(舍),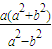 ,0).
,0).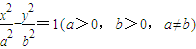 中,若E'为它的左顶点,M,N为双曲线Γ上的两点(都不同于点E'),且E'M⊥E'N,则直线MN过定点(
中,若E'为它的左顶点,M,N为双曲线Γ上的两点(都不同于点E'),且E'M⊥E'N,则直线MN过定点(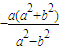 ,0).
,0).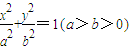 中,若E为它的右顶点,M,N为椭圆上的两点(都不同于点E),且EM⊥EN,则直线MN过定点(
中,若E为它的右顶点,M,N为椭圆上的两点(都不同于点E),且EM⊥EN,则直线MN过定点( ,0);
,0);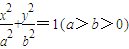 中,若E'为它的左顶点,M,N为椭圆上的两点(都不同于点E'),且E'M⊥E'N,则直线MN过定点(
中,若E'为它的左顶点,M,N为椭圆上的两点(都不同于点E'),且E'M⊥E'N,则直线MN过定点(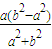 ,0);
,0);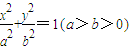 中,若F为它的上顶点,M,N为椭圆上的两点(都不同于点F),且FM⊥FN,则直线MN过定点(0,
中,若F为它的上顶点,M,N为椭圆上的两点(都不同于点F),且FM⊥FN,则直线MN过定点(0,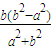 );
); 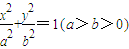 中,若F'为它的下顶点,M,N为椭圆上的两点(都不同于点F'),且F'M⊥F'N,则直线MN过定点(0,
中,若F'为它的下顶点,M,N为椭圆上的两点(都不同于点F'),且F'M⊥F'N,则直线MN过定点(0,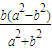 ).
).

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案