练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，曲线C的参数方程为（为参数），以原点O为极点，x轴正半轴为极轴建立极坐标系，直线的极坐标方程为，且直线与曲线C有两个不同的交点.

    （1）求实数a的取值范围；

    （2）已知M为曲线C上一点，且曲线C在点M处的切线与直线垂直，求点M的直角坐标.

    【答案】（1）；（2）或

    【解析】

    （1）分别求出曲线C与直线的直角坐标方程，由点到直线的距离公式即可得解；

    （2）设点，由题意可得即，结合同角三角函数的平方关系求得或后即可得解.

    （1）消参可得曲线C的普通方程为，可得曲线C是圆心为，半径为的圆，

    直线的直角坐标方程为，

    由直线与圆C有两个交点知，解得；

    （2）设圆C的圆心为，由圆C的参数方程可设点，由题知，∴，

    又，解得，或，

    故点M的直角坐标为或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:

    日期

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    天气

    晴

    雨

    阴

    阴

    阴

    雨

    阴

    晴

    晴

    晴

    阴

    晴

    晴

    晴

    晴

    日期

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    天气

    晴

    阴

    雨

    阴

    阴

    晴

    阴

    晴

    晴

    晴

    阴

    晴

    晴

    晴

    雨

    (1)在4月份任取一天,估计西安市在该天不下雨的概率;

    (2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在中，，点P为的中点，交于点D，现将沿翻折至，使得平面平面.

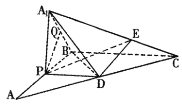
    （1）若Q为线段的中点，求证：平面；

    （2）在线段上是否存在点E，使得二面角大小为.若存在，请求出点E所在位置，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C1的参数方程为（为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为．

    （1）写出曲线C1和C2的直角坐标方程；

    （2）已知P为曲线C2上的动点，过点P作曲线C1的切线，切点为A，求|PA|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了判断英语词汇量与阅读水平是否相互独立，某语言培训机构随机抽取了100位英语学习者进行调查，经过计算的观测值为7，根据这一数据分析，下列说法正确的是（ ）

    附：

    0.050

    0.010

    0.005

    0.001

    3.841

    6.635

    7.879

    10.828

    A.有99%以上的把握认为英语词汇量与阅读水平无关

    B.有99.5%以上的把握认为英语词汇量与阅读水平有关

    C.有99.9%以上的把握认为英语词汇量与阅读水平有关

    D.在犯错误的概率不超过1%的前提下，可以认为英语词汇量与阅读水平有关

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知为椭圆的上顶点，P为椭圆E上异于上、下顶点的一个动点．当点P的横坐标为时，．

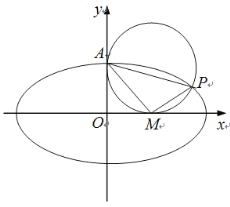
    （1）求椭圆E的标准方程；

    （2）设M为x轴的正半轴上的一个动点．

    ①若点P在第一象限内，且以AP为直径的圆恰好与x轴相切于点M，求AP的长．

    ②若，是否存在点N，满足，且AN的中点恰好在椭圆E上？若存在，求点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】天干地支纪年法，源于中国.中国自古便有十天干与十二地支.十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸，十二地支即子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配，排列起来，天干在前，地支在后，天干由“甲”起，地支由“子”起，比如说第一年为“甲子”，第二年为“乙丑”，第三年为“丙寅”… …依此类推，排列到“癸酉”后，天干回到“甲”重新开始，即“甲戌”“乙亥”，之后地支回到“子”重新开始，即“丙子”… …依此类推.1911年中国爆发推翻清朝专制帝制、建立共和政体的全国性革命,这一年是辛亥年，史称“辛亥革命”.1949新中国成立，请推算新中国成立的年份为( )

    A.己丑年B.己酉年

    C.丙寅年D.甲寅年

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一饮料店制作了一款新饮料，为了进行合理定价先进行试销售，其单价（元）与销量（杯）的相关数据如下表：

    单价（元）

    8.5

    9

    9.5

    10

    10.5

    销量（杯）

    120

    110

    90

    70

    60

    （1）已知销量与单价具有线性相关关系，求关于的线性回归方程；

    （2）若该款新饮料每杯的成本为8元，试销售结束后，请利用（1）所求的线性回归方程确定单价定为多少元时，销售的利润最大？（结果四舍五入保留到整数）

    附：线性回归方程中斜率和截距最小二乗法估计计算公式：，，，.

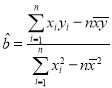    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.（其中为自然对数的底数）

    （1）当时，是否存在唯一的的值，使得？并说明理由；

    （2）若存在，使得对任意的恒成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案