
分析 (1)化简集合A,求出m=3时集合B,再根据补集与交集的定义写出运算结果;
(2)根据交集的定义,得出4是方程x2-2x-m=0,从而求出m的值.
解答 解:集合$A=\{x\left|{\frac{x-5}{x+1}≤0}\right.\}$={x|-1<x≤5},
B={x|x2-2x-m<0}.
(1)当m=3时,B={x|x2-2x-3<0}={x|-1<x<3}
∴∁RB={x|x≤-1或x≥3},
∴(∁RB)∩A={x|3≤x≤5};
(2)若A∩B={x|-1<x<4},
则4是方程x2-2x-m=0的实数根,
解得m=42-2×4=8.
点评 本题考查了集合的化简与运算问题,也考查了不等式与方程的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
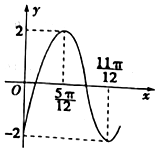 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | 5 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,总有2x≤1 | B. | ?x≤0,总有2x≤1 | C. | ?x≤0,使得2x≤1 | D. | ?x>0,使得2x≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$λ\overrightarrow{a}+μ\overrightarrow{b}$=$\overrightarrow{0}$,则λ=μ=0 | B. | 若$\overrightarrow{a}•\overrightarrow{b}$=0,则$\overrightarrow{a}$∥$\overrightarrow{b}$ | ||
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为|$\overrightarrow{a}$| | D. | 若$\overrightarrow{a}⊥\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{b}$=($\overrightarrow{a}$$•\overrightarrow{b}$)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-5+\sqrt{51}}{2}$ | B. | $\frac{-5+\sqrt{61}}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{2\sqrt{2}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com