
【题目】如果无穷数列{an}满足条件:①![]() ;② 存在实数M,使得an≤M,其中n∈N*,那么我们称数列{an}为Ω数列.
;② 存在实数M,使得an≤M,其中n∈N*,那么我们称数列{an}为Ω数列.
(1)设数列{bn}的通项为bn=20n-2n,且是Ω数列,求M的取值范围;
(2)设{cn}是各项为正数的等比数列,Sn是其前n项和,c3=![]() ,S3=
,S3=![]() ,证明:数列{Sn}是Ω数列;
,证明:数列{Sn}是Ω数列;
(3)设数列{dn}是各项均为正整数的Ω数列,求证:dn≤dn+1.
【答案】(1)![]() ;(2)证明见解析;(3)证明见解析
;(2)证明见解析;(3)证明见解析
【解析】
(1)求出数列![]() 的最大项即可得;
的最大项即可得;
(2)由等比数列的基本量法求出![]() ,根据数列新定义证明即可;
,根据数列新定义证明即可;
(3)用反证法,假设存在正整数![]() ,使得
,使得![]() ,由数列{dn}是各项均为正整数得
,由数列{dn}是各项均为正整数得![]() ,即
,即![]() .然后利用新定义归纳
.然后利用新定义归纳![]() ,这样由
,这样由![]() 可得数列从某一项开始为负.与已知矛盾.从而证得结论.
可得数列从某一项开始为负.与已知矛盾.从而证得结论.
解:(1)因为bn=20n-2n,所以![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以数列{bn}的最大项是![]() ,
,
所以![]() ,所以M的取值范围是
,所以M的取值范围是![]() .
.
(2)设{cn}的公比为![]() ,则
,则![]() ,c3=
,c3=![]() ,
,
整理得![]() ,解得
,解得![]() 或
或![]() ,因为
,因为![]() ,所以
,所以![]() .
.
因为{cn}是等比数列,所以
所以![]()
![]()
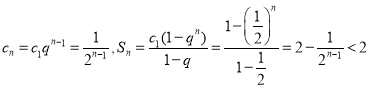 .
.
因为![]() ,所以数列{Sn}是Ω数列.
,所以数列{Sn}是Ω数列.
(3)假设存在正整数![]() ,使得
,使得![]() ,由数列{dn}是各项均为正整数得
,由数列{dn}是各项均为正整数得![]() ,即
,即![]() .
.
因为数列{dn}是Ω数列,所以![]() ,
,
所以![]() ,
,
同理,![]() ,
,
依此类推,得![]() .
.
因为数列{dn}是Ω数列,所以存在![]() ,
,![]() ,所以当
,所以当![]() 时,
时,![]() ,与数列{dn}各项均为正整数矛盾,所以假设不成立,即对任意的正整数
,与数列{dn}各项均为正整数矛盾,所以假设不成立,即对任意的正整数![]() ,dn≤dn+1
,dn≤dn+1


科目:高中数学 来源: 题型:
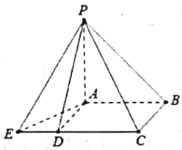
【题目】中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,若鳖臑
,若鳖臑![]() 的外接球的体积为
的外接球的体积为![]() ,则阳马
,则阳马![]() 的外接球的表面积等于______。
的外接球的表面积等于______。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线![]() 与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意x∈R,存在函数f(x)满足( )
A.f(cosx)=sin2xB.f(sin2x)=sinx
C.f(sinx)=sin2xD.f(sinx)=cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C1的极坐标方程为ρ=4cosθ,直线C2的参数方程为![]() (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程和直线C2的普通方程;
(2)若P(1,0),直线C2与曲线C1相交于A,B两点,求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在本题中,我们把具体如下性质的函数![]() 叫做区间
叫做区间![]() 上的闭函数:①
上的闭函数:①![]() 的定义域和值域都是
的定义域和值域都是![]() ;②
;②![]() 在
在![]() 上是增函数或者减函数.
上是增函数或者减函数.
(1)若![]() 在区间
在区间![]() 上是闭函数,求常数
上是闭函数,求常数![]() 的值;
的值;
(2)找出所有形如![]() 的函数(
的函数(![]() 都是常数),使其在区间
都是常数),使其在区间![]() 上是闭函数.
上是闭函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现给出两个条件:①![]() ,②
,②![]() ,从中选出一个条件补充在下面的问题中,并以此为依据求解问题:(选出一种可行的条件解答,若两个都选,则按第一个解答计分)在
,从中选出一个条件补充在下面的问题中,并以此为依据求解问题:(选出一种可行的条件解答,若两个都选,则按第一个解答计分)在![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边( ).
所对的边( ).
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知多面体ABCDEF中,四边形ABFE为正方形,![]() ,
,![]() ,G为AB的中点,
,G为AB的中点,![]() .
.

(1)求证:![]() 平面CDEF;
平面CDEF;
(2)求平面ACD与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com