
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的一点.
上的一点.

(1)若![]() 为
为![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)当点![]() 在什么位置时,
在什么位置时,![]() 平面
平面![]() .
.
【答案】(1)证明见解析;(2)![]() 为靠近
为靠近![]() 点的三等分点.
点的三等分点.
【解析】
(1)连接![]() 、
、![]() ,由中位线的性质得出
,由中位线的性质得出![]() ,可得出
,可得出![]() 平面
平面![]() ,证明四边形
,证明四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,进而得出
,进而得出![]() 平面
平面![]() ,再利用面面平行的判定定理可证明出平面
,再利用面面平行的判定定理可证明出平面![]() 平面
平面![]() ;
;
(2)连接![]() 、
、![]() ,设
,设![]() ,利用相似三角形得出
,利用相似三角形得出![]() ,由
,由![]() 平面
平面![]() 结合线面平行的性质得出
结合线面平行的性质得出![]() ,再利用平行线分线段成比例定理可确定点
,再利用平行线分线段成比例定理可确定点![]() 的位置.
的位置.
(1)如下图所示,连接![]() 、
、![]() ,
,
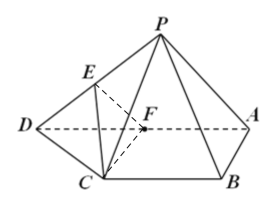
因为![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以
的中点,所以![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以,
,所以,![]() 平面
平面![]() ,
,
又因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ;
;
(2)连接![]() 、
、![]() ,设
,设![]() ,连接
,连接![]() ,
,
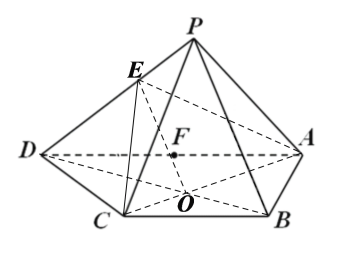
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,
,
![]() ,所以
,所以![]() .
.
在梯形![]() 中,
中,![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 为线段
为线段![]() 上靠近
上靠近![]() 点的三等分点.
点的三等分点.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为![]() ,已知
,已知![]() 且
且![]() .
.
(1)求角![]() ;
;
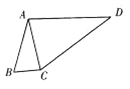
(2)如图,D为△ABC外一点,若在平面四边形ABCD中,![]() ,求△ACD面积的最大值.
,求△ACD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asin2x﹣2cos2x+1(a∈R)的图象经过点(﹣![]() ,1)
,1)
(1)求a;
(2)若在区间[0,m]上存在唯一实数x0,使得f(x0)=2,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣axlnx.
(1)当a=1时,求曲线f(x)在x=1处的切线方程;
(2)证明:对于a∈(0,e),函数f(x)在区间(![]() )上单调递增.
)上单调递增.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A、B两种产品,生产每一吨产品所需的劳动力和煤、电耗如下表:
产品品种 | 劳动力 | 煤 | 电 |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现在条件有限,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问:该企业生产A、B两种产品各多少吨,才能获得最大利润?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com