
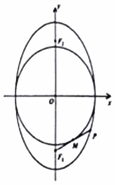
 若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点.
若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点.分析 (I)由椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9),可得a=3,b=$\sqrt{m}$.不妨设椭圆的下焦点为F1,设线段PF1的中点为M,则OM⊥PF1.利用中位线定理可得|PF2|=2b.由椭圆定义可得:|PF2|=2a-2b=6-2b.在Rt△OMF1中,利用勾股定理可得c2=b2+(3-b)2,又c2=a2-b2,解得b2.即可得出.
(II)椭圆的上焦点为:F2$(0,\sqrt{5})$.设直线l的方程为:y=kx+$\sqrt{5}$,A(x1,y1),B(x2,y2).与椭圆方程联立化为:$(4{k}^{2}+9){x}^{2}+8\sqrt{5}$kx-16=0,△>0.以AB为直径的圆经过点(0,-$\sqrt{5}$),可得$\overrightarrow{{F}_{1}A}$$•\overrightarrow{{F}_{1}B}$=0,可得x1x2+$({y}_{1}+\sqrt{5})$$({y}_{2}+\sqrt{5})$=x1x2+$(k{x}_{1}+2\sqrt{5})$$(k{x}_{2}+2\sqrt{5})$=0,把根与系数的关系代入即可得出.
解答 解:(I)由椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9),可得a=3,b=$\sqrt{m}$.
不妨设椭圆的下焦点为F1,设线段PF1的中点为M,则OM⊥PF1.
又OM=b,OM是△PF1F2的中位线,∴|PF2|=2b.
由椭圆定义可得:|PF2|=2a-2b=6-2b.∴|MF1|=$\frac{1}{2}|P{F}_{1}|$=3-b.
在Rt△OMF1中,$|O{F}_{1}{|}^{2}$=|OM|2+$|M{F}_{1}{|}^{2}$.∴c2=b2+(3-b)2,
又c2=a2-b2=9-b2,∴b2+(3-b)2=9-b2,解得b=2,∴m=b2=4.
∴椭圆C的方程为:$\frac{{y}^{2}}{9}+\frac{{x}^{2}}{4}$=1.
(II)椭圆的上焦点为:F2$(0,\sqrt{5})$.设直线l的方程为:y=kx+$\sqrt{5}$,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=kx+\sqrt{5}}\\{\frac{{y}^{2}}{9}+\frac{{x}^{2}}{4}=1}\end{array}\right.$,化为:$(4{k}^{2}+9){x}^{2}+8\sqrt{5}$kx-16=0,△>0.∴x1+x2=$\frac{-8\sqrt{5}k}{4{k}^{2}+9}$,x1•x2=$\frac{-16}{4{k}^{2}+9}$,
∵以AB为直径的圆经过点(0,-$\sqrt{5}$),∴$\overrightarrow{{F}_{1}A}$$•\overrightarrow{{F}_{1}B}$=0,
∴x1x2+$({y}_{1}+\sqrt{5})$$({y}_{2}+\sqrt{5})$=x1x2+$(k{x}_{1}+2\sqrt{5})$$(k{x}_{2}+2\sqrt{5})$=(1+k2)x1x2+$2\sqrt{5}$k(x1+x2)+20
=(1+k2)•$\frac{-16}{4{k}^{2}+9}$+2$\sqrt{5}$k×$\frac{-8\sqrt{5}k}{4{k}^{2}+9}$+20=$\frac{-16{k}^{2}+164}{4{k}^{2}+9}$=0,
解得k=$±\frac{\sqrt{41}}{2}$,
∴直线l的方程为y=$±\frac{\sqrt{41}}{2}$x+$\sqrt{5}$.
点评 本题考查了椭圆的定义标准方程、直线与椭圆相交问题、一元二次方程的根与系数的关系、向量垂直与数量积的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1364 | B. | $\frac{124}{3}$ | C. | 118 | D. | 124 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x2≥1,则-1≥x≥1 | B. | 若1≥x≥-1,则x2≥1 | ||
| C. | 若x≤-1或x≥1,则x2≥1 | D. | 若x2≥1,则x≤-1或x≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com