
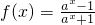 (a>0且a≠1).
(a>0且a≠1).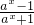 ,解得ax=-
,解得ax=-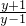 ①
①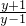 >0时,方程①有解.解-
>0时,方程①有解.解-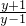 >0,求得-1<y<1.
>0,求得-1<y<1.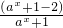 =1-
=1-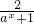 .
.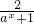 为减函数,从而f(x)=1-
为减函数,从而f(x)=1-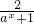 =
=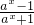 为增函数.
为增函数.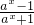 为减函数.
为减函数. ≤4,∴2≤f(x2)=2+
≤4,∴2≤f(x2)=2+ ≤6.
≤6.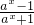 ,解得ax=-
,解得ax=-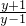 ①,根据ax>0,可得当且仅当-
①,根据ax>0,可得当且仅当-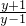 >0时,方程①有解.解-
>0时,方程①有解.解-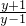 >0,求得y的范围.
>0,求得y的范围.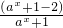 =1-
=1-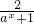 ,分当a>1时和 当0<a<1时,两种情况,分别研究函数的单调性.
,分当a>1时和 当0<a<1时,两种情况,分别研究函数的单调性. ≤6.由此求得函数y=[f(x)]2+f(x2)的最大值和最小值.
≤6.由此求得函数y=[f(x)]2+f(x2)的最大值和最小值.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年甘肃省庆阳市宁县二中高一(上)第一次月考数学试卷(解析版) 题型:解答题
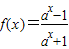 (a>0且a≠1).
(a>0且a≠1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com