
【题目】(12分)
如图,四棱锥P-ABCD中,侧面PAD为等比三角形且垂直于底面ABCD,![]() E是PD的中点.
E是PD的中点.

(1)证明:直线![]() 平面PAB
平面PAB
(2)点M在棱PC 上,且直线BM与底面ABCD所成锐角为![]() ,求二面角M-AB-D的余弦值
,求二面角M-AB-D的余弦值
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】已知sinα+cosα= ![]() ,α∈(0,
,α∈(0, ![]() ),sin(β﹣
),sin(β﹣ ![]() )=
)= ![]() ,β∈(
,β∈( ![]() ,
, ![]() ).
).
(1)求sin2α和tan2α的值;
(2)求cos(α+2β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若 {an}是等比数列,a4a7=﹣512,a3+a8=124,且公比q为整数,则a10=( )
A.256
B.﹣256
C.512
D.﹣512
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示;
)的部分图象如图所示; 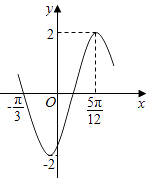
(1)求ω,φ;
(2)将y=f(x)的图象向左平移θ(θ>0)个单位长度,得到y=g(x)的图象,若y=g(x)图象的一个对称点为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.
(3)对任意的x∈[ ![]() ,
, ![]() ]时,方程f(x)=m有两个不等根,求m的取值范围.
]时,方程f(x)=m有两个不等根,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形. 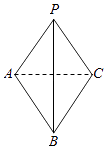
(1)证明:AB⊥PC;
(2)若AB=2PC= ![]() ,求三棱锥P﹣ABC的体积.
,求三棱锥P﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,BC=2AB=4, ![]() ,E是A1D1的中点.
,E是A1D1的中点.
(Ⅰ)在平面A1B1C1D1内,请作出过点E与CE垂直的直线l,并证明l⊥CE;
(Ⅱ)设(Ⅰ)中所作直线l与CE确定的平面为α,求点C1到平面α的距离.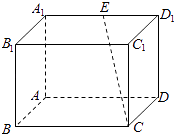
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM,E为BD的中点. 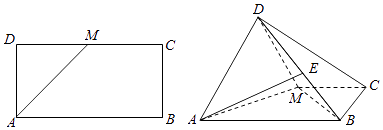
(1)求证:BM⊥平面ADM;
(2)求直线AE与平面ADM所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com