
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,短轴长为2.直线l:y=kx+m与椭圆C交于M,N两点,又l与直线
,短轴长为2.直线l:y=kx+m与椭圆C交于M,N两点,又l与直线![]() ,
, ![]() 分别交于A,B两点,其中点A在第一象限,点B在第二象限,且△OAB的面积为2(O为坐标原点).
分别交于A,B两点,其中点A在第一象限,点B在第二象限,且△OAB的面积为2(O为坐标原点).
(1)求椭圆C的方程;
(2)求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:
(1)由离心率及![]() 可得
可得![]() ,于是可得椭圆的方程.(2)结合题意逐步求解,先求得点A,B的坐标,并根据点的位置得到
,于是可得椭圆的方程.(2)结合题意逐步求解,先求得点A,B的坐标,并根据点的位置得到![]() ;然后根据直线与椭圆的位置关系可得
;然后根据直线与椭圆的位置关系可得![]() ,于是
,于是![]() .由△OAB的面积为2计算可得
.由△OAB的面积为2计算可得![]() ,最后根据数量积的定义将
,最后根据数量积的定义将![]() 用
用![]() 表示,并可得到所求范围.
表示,并可得到所求范围.
试题解析:
(1)∵离心率e=![]() ,
, ![]() ,
,
∴![]() =
=![]() =
=![]() ,解得a2=2,
,解得a2=2,
∴椭圆的方程为![]() +y2=1.
+y2=1.
(2)由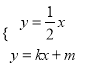 可得点A的坐标为
可得点A的坐标为 ![]() ,
,
由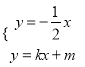 可得点B的坐标为
可得点B的坐标为![]() ,
,
又点A在第一象限,点B在第二象限,
∴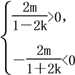 即
即![]()
∴m2(1-4k2)>0,
又m2≥0,
∴1-4k2>0.
∵|AB|=![]() =
=![]()
![]() ,
,
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即△OAB底边AB上的高为
,即△OAB底边AB上的高为![]() ,
,
∴S△OAB=![]() ·
·![]() ·
·![]() =
= ![]() = 2,
= 2,
∴m2=1-4k2.
由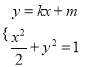 消去y整理得(1+2k2)x2+4kmx+2m2-2=0,
消去y整理得(1+2k2)x2+4kmx+2m2-2=0,
∵直线![]() 与椭圆交于两点,
与椭圆交于两点,
∴Δ=16k2m2-4(1+2k2)(2m2-2)=48k2>0,解得k2>0.
设M(x1,y1),N(x2,y2),
则x1+x2=-![]() ,x1·x2=
,x1·x2=![]() ,
,
∴y1·y2=(kx1+m)(kx2+m)=![]() ,
,
∴![]() ·
·![]() =x1x2+y1y2=
=x1x2+y1y2=![]() +
+![]() =
=![]() -7.
-7.
∵0<k2<![]() ,
,
∴1+2k2∈![]() ,
,
∴![]() ∈
∈![]() ,
,
∴![]() ·
·![]() ∈
∈![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆的极坐标方程为:ρ2-4![]() ρcos(θ-
ρcos(θ-![]() )+6=0.
)+6=0.
(1)将极坐标方程化为普通方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: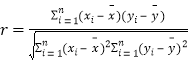 ,回归直线方程是
,回归直线方程是![]() ,
,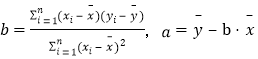 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖促销活动,规定每位顾客从装有编号为0,1,2,3四个相同小球的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码之和等于6,则中一等奖,等于5中二等奖,等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com