£ØĪÄæĘ£©ŅŃÖŖn2£Øn”Ż4ĒŅn”ŹN*£©øöÕżŹżÅųÉŅ»øönŠŠnĮŠµÄŹżÕó£ŗ
””””””””””µŚ1ĮŠ”” µŚ2ĮŠ””””µŚ3ĮŠ”” ”µŚnĮŠ
µŚ1ŠŠ”””” a1£¬1 a1£¬2 a1£¬3 ”a1£¬n
µŚ2ŠŠ”””” a2£¬1 a2£¬2 a2£¬3 ”a2£¬n
µŚ3ŠŠ”””” a3£¬1 a3£¬2 a3£¬3 ”a3£¬n
”
µŚnŠŠ”””” an£¬1 an£¬2 an£¬3 ”an£¬n
ĘäÖŠai£¬k£Øi£¬k”ŹN*£¬ĒŅ1”Üi”Ün£¬1”Ük”Ün£©±ķŹ¾øĆŹżÕóÖŠĪ»ÓŚµŚiŠŠµŚkĮŠµÄŹż£¬ŅŃÖŖøĆŹżÕóÖŠø÷ŠŠµÄŹżŅĄ“Ī³ÉµČ±ČŹżĮŠ£¬ø÷ĮŠµÄŹżŅĄ“Ī³É¹«±ČĪŖ2µÄµČ±ČŹżĮŠ£¬ŅŃÖŖa2£¬3=8£¬a3£¬4=20£®
£Ø1£©Ēóa1£¬1a2£¬2£»
£Ø2£©ÉčAn=a1£¬n+a2£¬n-1+a3£¬n-2+”+an£¬1ĒóÖ¤£ŗAn+nÄܱ»3Õū³ż£®
½ā£ŗ£Ø1£©ÓÉĢāŅā£¬a
2£¬3=8£¬
a
3£¬4=20£¬
ĖłŅŌa
1£¬3=3£¬a
1£¬4=5£¬
¹ŹµŚ1ŠŠ¹«²īd=1£¬
ĖłŅŌa
1£¬1=2£¬a
1£¬2=3£¬
µĆa
2£¬2=2a
1£¬2=6£®
£Ø2£©Ķ¬£Ø1£©æÉµĆ£¬a
1£¬n=n+1£¬a
2£¬n-1
=2n£¬a
3£¬n-2
=2
2£Øn-1£©£¬”£¬a
n-1£¬2
=3”Į2
n-2£¬a
n£¬1
=2”Į2
n-1ĖłŅŌA
n=a
1£¬n+a
2£¬n-1+a
3£¬n-2+”+a
n£¬1
=£Øn+1£©+n”Į2
1+£Øn-1£©”Į2
2+£Øn-2£©”Į2
3+”+2”Į2
n-12A
n
=£Øn+1£©”Į2
1+n”Į2
2+£Øn-1£©”Į2
3+”+3”Į2
n-1+2”Į2
n
Į½Ź½Ļą¼õ£¬µĆA
n=-£Øn+1£©+2
1+2
2+2
3+”+2
n-1+2”Į2
n
=
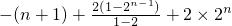
=-£Øn+1£©+2
n-2+2”Į2
n
=3”Į2
n-3-n
ĖłŅŌA
n-n=3”Į£Ø2
n-1£©£¬
¹ŹA
n+nÄܱ»3Õū³ż£®
·ÖĪö£ŗ£Ø1£©ÓÉĢāŅā£¬a
2£¬3=8£¬a
3£¬4=20£¬ĖłŅŌa
1£¬3=3£¬a
1£¬4=5£¬¹ŹµŚ1ŠŠ¹«²īd=1£¬ÓÉ“ĖÄÜĒó³öa
1£¬1ŗĶa
2£¬2£®
£Ø2£©ÓÉa
1£¬n=n+1£¬a
2£¬n-1=2n£¬a
3£¬n-2=2
2£Øn-1£©£¬”£¬a
n-1£¬2=3”Į2
n-2£¬a
n£¬1=2”Į2
n-1£¬ÖŖA
n=a
1£¬n+a
2£¬n-1+a
3£¬n-2+”+a
n£¬1=£Øn+1£©+n”Į2
1+£Øn-1£©”Į2
2+£Øn-2£©”Į2
3+”+2”Į2
n-1£¬ÓÉ“ķĪ»Ļą¼õ·ØÄܹ»Ēó³öA
n£®ÓÉ“ĖÄܹ»Ö¤Ć÷A
n+nÄܱ»3Õū³ż£®
µćĘĄ£ŗ±¾Ģāæ¼²éŹżĮŠµÄ×ŪŗĻŌĖÓĆ£¬×ŪŗĻŠŌĒ棬ÄŃ¶Č½Ļ“ó£¬ČŻŅ׳ö“ķ£®½āĢāŹ±ŅŖČĻÕęÉóĢā£¬×¢ŅāŃ°ÕŅ¹ęĀÉ£¬ŗĻĄķµŲ½ųŠŠµČ¼Ū×Ŗ»Æ£®
æĘÄæ£ŗøßÖŠŹżŃ§
Ą“Ō“£ŗ2007-2008ѧğ½ĖÕŹ”ÄĻ¾©ŹŠ½šĮźÖŠŃ§øßČż£ØÉĻ£©ÖŹĮæ¼ģ²āŹżŃ§ŹŌ¾ķ£ØĪÄĄķŗĻ¾ķ£©£Ø½āĪö°ę£©
ĢāŠĶ£ŗ½ā“šĢā
£ØĪÄæĘ£©ŅŃÖŖn2£Øn”Ż4ĒŅn”ŹN*£©øöÕżŹżÅųÉŅ»øönŠŠnĮŠµÄŹżÕó£ŗ
µŚ1ĮŠ µŚ2ĮŠ µŚ3ĮŠ ”µŚnĮŠ
µŚ1ŠŠ a1£¬1 a1£¬2 a1£¬3 ”a1£¬n
µŚ2ŠŠ a2£¬1 a2£¬2 a2£¬3 ”a2£¬n
µŚ3ŠŠ a3£¬1 a3£¬2 a3£¬3 ”a3£¬n
”
µŚnŠŠ an£¬1 an£¬2 an£¬3 ”an£¬n
ĘäÖŠai£¬k£Øi£¬k”ŹN*£¬ĒŅ1”Üi”Ün£¬1”Ük”Ün£©±ķŹ¾øĆŹżÕóÖŠĪ»ÓŚµŚiŠŠµŚkĮŠµÄŹż£¬ŅŃÖŖøĆŹżÕóÖŠø÷ŠŠµÄŹżŅĄ“Ī³ÉµČ±ČŹżĮŠ£¬ø÷ĮŠµÄŹżŅĄ“Ī³É¹«±ČĪŖ2µÄµČ±ČŹżĮŠ£¬ŅŃÖŖa2£¬3=8£¬a3£¬4=20£®
£Ø1£©Ēóa1£¬1a2£¬2£»
£Ø2£©ÉčAn=a1£¬n+a2£¬n-1+a3£¬n-2+”+an£¬1ĒóÖ¤£ŗAn+nÄܱ»3Õū³ż£®
²éæ““š°øŗĶ½āĪö>>



 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø