
 ,函数
,函数 .
. 时,求使
时,求使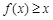 成立的
成立的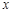 的集合;
的集合; 在区间
在区间 上的最小值.
上的最小值.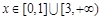 ;
;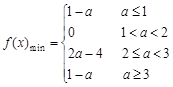 。
。 .故当
.故当 时,求使
时,求使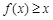 成立的
成立的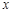 的集合,只需要对x分情况讨论既可以得到。
的集合,只需要对x分情况讨论既可以得到。 在区间
在区间 上的最小值,分析对称轴和定义域的关系,分类讨论得到结论。
上的最小值,分析对称轴和定义域的关系,分类讨论得到结论。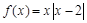 . …………………………………………1分
. …………………………………………1分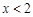 时,
时,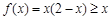 ,解得
,解得 ; ……………………………2分
; ……………………………2分 时,
时,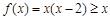 ,解得
,解得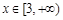 . ……………………………3分
. ……………………………3分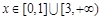 ……………………………………………………4分
……………………………………………………4分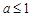 时,在区间
时,在区间 上,
上,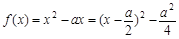 ,其图像是开口向上的抛物线,对称轴是
,其图像是开口向上的抛物线,对称轴是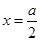 ,
,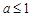 ,
,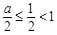 ,
,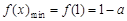 ……………………………………………………6分
……………………………………………………6分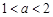 时,在区间[1,2]上,
时,在区间[1,2]上,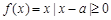 ,
, ……8分
……8分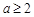 时,在区间[1,2]上,
时,在区间[1,2]上,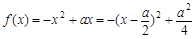 ,其图像是开口向下的抛物线,对称轴是
,其图像是开口向下的抛物线,对称轴是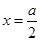 ,
, 当
当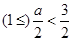 即
即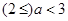 时,
时,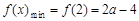 …………10分
…………10分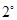 当
当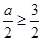 即
即 时,
时,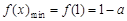
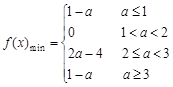 …………………………………………12分
…………………………………………12分

科目:高中数学 来源:不详 题型:解答题
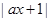 (a∈R),不等式f(x)≤3的解集为{x|?2≤x≤1}.
(a∈R),不等式f(x)≤3的解集为{x|?2≤x≤1}.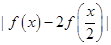 ≤k恒成立,求k的取值范围.
≤k恒成立,求k的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.|a|>|b|-|c| | B.|a|<|b|+|c| | C.a>c-b | D.a<b+c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com