练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函f（x）数满足f（x+1）=-f（x），当x∈（0，1）时，f（x）=2x，则x∈（-3，-2）时，f（x）=
    -2x+3
    -2x+3
    ．
    分析：由f（x+1）=-f（x）得函数的周期性，求x∈（-3，-2）的解析式转化成（0，1）范围内，代入已知解析式即得．
    解答：解：∵f（x+1）=-f（x）
    ∴f（x+2）=f（x）即f（x）是周期为2的函数
    设x∈（-3，-2）则x+3∈（0，1）
    ∴f（x+3）=f（x+1）=-f（x）=2x+3，
    即f（x）=-2x+3
    故答案为-2x+3
    点评：本题主要考查了利用周期性求解函数解析式，通过未知转化到已知进行求解，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    已知函f（x）数满足f（x+1）=-f（x），当x∈（0，1）时，f（x）=2x，则x∈（-3，-2）时，f（x）=________．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江西省高三第一次统考理科数学 题型：填空题

    若直角坐标平面内A、B两点满足条件：①点A、B都在f(x)的图象上；②点A、B关于原点对称，

    则对称点对(A、B)是函数的一个“姊妹点对”(点对(A，B)与（B，A）可看作同一个“姊妹点对”)已知函

    数 f(x)=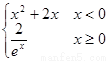，则f(x)的“姊妹点对”有       个。

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年广东省高三上学期第三次月考理科数学 题型：解答题

    （本小题满分12分）

    已知向量，函数·，

    (1)求函数f（x）的单调递增区间；

    (2)如果△ABC的三边a、b、c满足b2=ac，且边b所对的角为x，试求x的范围及此时函

    数f（x）的值域．

     

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年度新课标高三上学期数学单元测试5-理科-平面向量与解三角形 题型：解答题

     

    已知向量m＝（，），n＝(，)，记f(x)=m•n；

       （1）若f(x)=1,求的值；

       （2）若△ABC中，角A，B，C的对边分别是a,b,c，且满足（2a-c）cosB=bcosC，求函

            数f(A)的取值范围．

     

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案