
����Ŀ�����Ž�������̼��������������г����ε���Խ��Խ��.ij���г������շѱ���ÿ��ÿ����ʱ�䲻������Сʱ��ѣ���������Сʱ�IJ���ÿСʱ�շ�2Ԫ������1Сʱ�IJ��ְ�1Сʱ���㣩.�мס������˶�������������Σ�����һ��һ�Σ�.��ס��Ҳ�������Сʱ�����ĸ��ʷֱ�Ϊ![]() ��
�� ![]() ����Сʱ�����Ҳ�������Сʱ�����ĸ��ʷֱ�Ϊ
����Сʱ�����Ҳ�������Сʱ�����ĸ��ʷֱ�Ϊ![]() ��
�� ![]() �������ʱ�䶼���ᳬ����Сʱ.
�������ʱ�䶼���ᳬ����Сʱ.
��1����ס������������������ͬ�ĸ��ʣ�
��2����ס������������������֮��Ϊ�������![]() ����
����![]() �ķֲ���.
�ķֲ���.
���𰸡���1��![]() ��2��������
��2��������
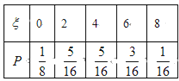
�������������������1��������ɵã��ס���ʹ��ʱ�������
��0��2 | ��2��3 | ��3��4 | |
�� |
|
|
|
�� |
|
|
|
���Գ�����ͬ����ʹ��ʱ��һ�����ֳ����������¼�����ʱ��0��2![]() ����2��3
����2��3![]() ����3��4
����3��4![]()
���ݻ����¼��ĺ��¼���������¼�ͬʱ���ĸ��ʹ�ʽ�ɵ�![]() ����2��������ɵ�
����2��������ɵ�![]() ����ȡ��ֵΪ0��2��4��6��8������0Ԫ������0,0����2Ԫ������0,2������2,0����4Ԫ����(0,4),(4,0),(2,2),6Ԫ����(4,2),(2,4), 8Ԫ����(4,4), ���ݻ����¼��ĺ��¼���������¼�ͬʱ���ĸ��ʹ�ʽ�ֱ����ɵá�
����ȡ��ֵΪ0��2��4��6��8������0Ԫ������0,0����2Ԫ������0,2������2,0����4Ԫ����(0,4),(4,0),(2,2),6Ԫ����(4,2),(2,4), 8Ԫ����(4,4), ���ݻ����¼��ĺ��¼���������¼�ͬʱ���ĸ��ʹ�ʽ�ֱ����ɵá�
�����������1��������ã��ף�������Сʱ�����Ҳ�������Сʱ�����ĸ��ʷֱ�Ϊ![]() ��
�� ![]() ��
��
�Ǽס��������������������ͬΪ�¼�����
![]() ��
��
���ԣ��ס��������������������ͬ�ĸ���Ϊ![]() ��
��
��2����ס������������ķ���֮��Ϊ![]() ��
�� ![]() ����ȡ��ֵΪ0��2��4��6��8
����ȡ��ֵΪ0��2��4��6��8
![]() ��
�� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
��
�ֲ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f��x������СֵΪ1����f��0��=f��2��=3��
��1����f��x���Ľ���ʽ��
��2����f��x��������[2a��a+1]�ϲ���������a��ȡֵ��Χ
��3����x��[t��t+2]������y=f��x������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����GΪ��ABC�����ģ���G��ֱ��l�ֱ��߶�AB��AC������˵��غϣ���P��Q���� ![]() =��
=�� ![]() ��
�� ![]() =��
=�� ![]() ��
�� 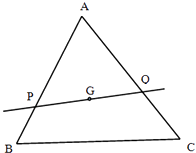
��1���� ![]() ��ֵ��
��ֵ��
��2����˦̵�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}��ǰn���ΪSn �� ��Sn=2n��1������{bn}����b1=2��bn+1��2bn=8an ��
��1��������{an}��ͨ�ʽ��
��2��֤��������{ ![]() }Ϊ�Ȳ����У�����{bn}��ͨ�ʽ��
}Ϊ�Ȳ����У�����{bn}��ͨ�ʽ��
��3����{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й��ڻع������˵���д�����ǣ� ��
A. �ع�ֱ��һ������������![]()
B. �в�ͼ�вв��ȽϾ��ȵ�����ˮƽ�Ĵ�״�����У�˵��ѡ�õ�ģ�ͱȽϺ���
C. ����ģ���вв�ƽ����ԽС��ģ����ϵ�Ч��Խ��
D. �ס�������ģ�͵�![]() �ֱ�ԼΪ0.98��0.80����ģ���ҵ����Ч������
�ֱ�ԼΪ0.98��0.80����ģ���ҵ����Ч������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ҹ�ĸ��¼��Ů���h�h�����䣨�꣩�����ߣ���λcm�����������£�
����x | 6 | 7 | 8 | 9 |
����y | 118 | 126 | 136 | 144 |
��1������y����x�����Իع鷽�� ![]() =
= ![]() x+
x+ ![]()
��2����Ԥ��h�h10��ʱ�����ߣ������У� ![]() =
=  ��
�� ![]() =
= ![]() ��
�� ![]()
![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��a1=t��n2Sn+1=n2��Sn+an��+an2 �� n=1��2������
��1����{an}Ϊ�Ȳ����У���ǰ�����S2=3����t��ֵ��
��2����t= ![]() ��֤����
��֤���� ![]() ��an��1��
��an��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��k��0����
��k��0����
��1����f��x����m�Ľ⼯Ϊ{x|x����3��x����2}����ʽ5mx2+ ![]() x+3��0�Ľ⼯��
x+3��0�Ľ⼯��
��2��������x��3ʹ��f��x����1��������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�ǵȲ����У���a1=2��a1+a2+a3=12��
��1��������{an}��ͨ�ʽ��
��2����bn=an3n��x��R����������{bn}ǰn��͵Ĺ�ʽ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com