
已知关于x的一元二次方程 (m∈Z)
① mx2-4x+4=0,
② x2-4mx+4m2-4m-5=0,求方程①和②都有整数解的充要条件.
 .
.
解析试题分析:(1)判定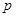 是
是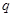 的什么条件,需要从两方面去理解:一是由条件
的什么条件,需要从两方面去理解:一是由条件 能否推得
能否推得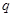 ;二是由条件
;二是由条件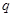 能否推得
能否推得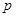 .对于带有否定性的命题或比较难判断的命题,除借助集合思想把抽象、复杂问题形象化、直观化外,还可以利用原命题和逆否命题、逆命题和否命题的等价性,转化为判断它的等价命题;(2)判断充要条件的方法:(1)定义法:直接判断若
.对于带有否定性的命题或比较难判断的命题,除借助集合思想把抽象、复杂问题形象化、直观化外,还可以利用原命题和逆否命题、逆命题和否命题的等价性,转化为判断它的等价命题;(2)判断充要条件的方法:(1)定义法:直接判断若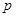 则
则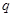 、若
、若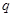 则
则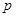 的真假;(2)等价法:利用
的真假;(2)等价法:利用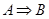 与
与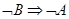 ,
,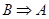 与
与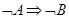 ,
,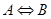 与
与 的等价关系,对于条件或结论是否定式的命题,一般运用等价法;(3)利用集合间的包含关系判断:若
的等价关系,对于条件或结论是否定式的命题,一般运用等价法;(3)利用集合间的包含关系判断:若 ,则
,则 是
是 的充分条件或
的充分条件或 是
是 的必要条件,若
的必要条件,若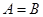 ,则
,则 是
是 的充要条件.
的充要条件.
试题解析:解:方程①有实根的充要条件是 解得m
解得m 1.
1.
方程②有实根的充要条件是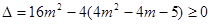 ,
,
解得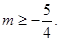
 故m=-1或m=0或m=1.
故m=-1或m=0或m=1.
当m=-1时,①方程无整数解.
当m=0时,②无整数解;
当m=1时,①②都有整数.从而①②都有整数解m=1.反之,m=1①②都有整数解.
∴①②都有整数解的充要条件是m=1
考点:充要条件的探索.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)在区间(-∞,+∞)上是增函数,a,b∈R.
(1)求证:若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b);
(2)判断(1)中命题的逆命题是否正确,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com