
| A. | b<a<c | B. | c<b<a | C. | b<c<a | D. | a<b<c |
分析 由题意和诱导公式化简cos$\frac{5}{7}$π、tan$\frac{5}{7}$π,根据偶函数的性质化简b、c,由三角函数的性质判断出tan$\frac{2}{7}π$、
sin$\frac{2}{7}π$、cos$\frac{2}{7}π$三者的大小关系,由偶函数的单调性和条件判断出f(x)在区间[0,+∞)上单调性,利用单调性可得答案.
解答 解:由$\frac{5}{7}π=π-\frac{2}{7}π$得,cos$\frac{5}{7}$π=-cos$\frac{2}{7}π$,tan$\frac{5}{7}$π=-tan$\frac{2}{7}π$,
∵函数f(x)是R上的偶函数,
∴b=f(cos$\frac{5}{7}$π)=f(cos$\frac{2}{7}π$),c=f(tan$\frac{5}{7}$π)=f(tan$\frac{2}{7}π$),
∵$\frac{2}{7}π>\frac{π}{4}$,∴tan$\frac{2}{7}π$>sin$\frac{2}{7}π$>cos$\frac{2}{7}π$,
∵偶函数f(x)在区间(-∞,0]上是减函数,∴函数f(x)在区间[0,+∞)上是增函数,
则f(tan$\frac{2}{7}π$)>f(sin$\frac{2}{7}π$)>f(cos$\frac{2}{7}π$),即c>a>b,
故选A.
点评 本题考查函数单调性、奇偶性的综合应用,以及诱导公式、三角函数的性质,解题的关键是利用函数对称性、奇偶性自变量调整到同一单调区间内,再比较大小,考查数形结合思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
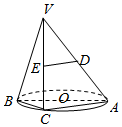 AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-2=0 | B. | x-y-2=0 | C. | x-y+2=0 | D. | x+y+2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三角形的内角是第一象限角或第二象限角 | |
| B. | 第一象限的角是锐角 | |
| C. | 第二象限的角比第一象限的角大 | |
| D. | 角α是第四象限角的充要条件是2kπ-$\frac{π}{2}$<α<2kπ(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[0,\frac{4}{27}]$ | B. | $[0,\frac{3}{8}]$ | C. | [-$\frac{9}{8}$,$\frac{4}{27}$] | D. | $[-\frac{9}{8},\frac{3}{8}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}$ | C. | $\root{4e}{e}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是最大、最小值点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0,则A=$\frac{π}{6}$.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是最大、最小值点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0,则A=$\frac{π}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com