练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的离心率为，且经过点.

    （1）求椭圆C的方程；

    （2）设过点的直线l与椭圆C交于，两点，求的取值范围.

    【答案】（1） （2）

    【解析】

    （1）将点代入椭圆方程，结合离心率公式，联立方程组，求解即可得出椭圆的方程；

    讨论直线l的斜率为0和不为0两种情况，当直线l的斜率为0时，，得出；

    当直线l的斜率不为0时，设出直线l的方程，代入椭圆方程，利用韦达定理得出，的值，进而得出，换元令，得出，由二次函数的性质求出的取值范围.

    解：（1）因为椭圆C经过点，所以，①

    因为椭圆C的离心率为，所以，所以.②

    由①②得，.

    故椭圆C的方程为.

    （2）①当直线l的斜率为0时，，所以.

    ②当直线l的斜率不为0时，设直线l的方程为.

    联立，整理得

    则，

    设，则，从而

    因为，所以，即

    综上的取值范围是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在中，边，，所在直线的方程分别为，，.

    （1）求边上的高所在的直线方程；

    （2）若圆过直线上一点及点，当圆面积最小时，求其标准方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数有两个零点，，则下列判断：①；②；③；④有极小值点，且.则正确判断的个数是（ ）

    A. 4个B. 3个C. 2个D. 1个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若直线y=a分别与直线y=2x-3，曲线y=ex-x（x≥0）交于点A，B，则|AB|的最小值为（　　）

    A. B. C. eD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若，求的单调区间；

    （2）若，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，几何体AMDCNB是由两个完全相同的四棱锥构成的几何体，这两个四棱锥的底面ABCD为正方形，，平面平面ABCD.

    (1)证明:平面平面MDC.

    (2)若，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中,直线的参数方程为 (为参数),曲线的参数方为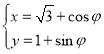 (为参数),以为极点, 轴的非负半轴为极轴建立极坐标系.

    (1)求直线和曲线的极坐标方程;

    (2)设,,为直线与曲线的两个交点,求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知倾斜角为的直线过点和点，在第一象限，；

    （1）求点的坐标；

    （2）若直线与两平行直线，相交于两点，且，求实数的值；

    （3）对于平面上任一点，当点在线段上运动时，称的最小值为与线段的距离，试求点，到线段的距离关于的函数关系式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“搜索指数”是网民通过搜索引擎，以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大，表示网民对该关键词的搜索次数越多，对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中，某个关键词的搜索指数变化的走势图.

    根据该走势图，下列结论正确的是（ ）

    A. 这半年中，网民对该关键词相关的信息关注度呈周期性变化

    B. 这半年中，网民对该关键词相关的信息关注度不断减弱

    C. 从网民对该关键词的搜索指数来看，去年10月份的方差小于11月份的方差

    D. 从网民对该关键词的搜索指数来看，去年12月份的平均值大于今年1月份的平均值

    查看答案和解析>>

    同步练习册答案